Create Calibration Plots — calibration

calibration_plot() generates a calibration plot to assess the performance of a model's probabilistic predictions.

Usage

calibration_plot(
  actual,
  predicted,
  breaks = seq(0, 1, by = 0.1),
  show_plot = TRUE,
  ...
)

Arguments

actual: a vector of true outcomes. Must be a numeric vector containing 0 and 1.
predicted: a numeric vector of predicted probabilities, typically ranging from 0 to 1.
breaks: a numeric vector of cut points used to bin the predicted values. Defaults to seq(0, 1, by = .1).
show_plot: logical. If TRUE (the default), a plot is displayed. If FALSE, the summary data is returned without plotting.
...: additional arguments passed to the plot() function. This can be used to customize the plot's title (main), color (col), point and line types (type), etc.

Value

If show_plot = TRUE, the function draws a plot as a side effect and invisibly returns a data frame with the summary statistics. If show_plot = FALSE, it visibly returns the data frame. The returned data frame includes the following columns:

bin: The bin number to which the predictions were assigned.
n: The number of observations in each bin.
actual: The mean of the true outcomes in each bin (i.e., the fraction of positives).
predicted: The mean of the predicted probabilities in each bin.

Details

The function groups predicted probabilities into bins by findInterval(predicted, breaks, rightmost.closed = TRUE, left.open = FALSE, all.inside = FALSE), and plots the mean predicted probability (x-axis) against the fraction of positive actual outcomes (y-axis) for each bin. A perfectly calibrated model would have points lying on the diagonal line \(y = x\), indicating that a predicted probability of, for example, 0.8 corresponds to an 80 percent proportion of positive outcomes.

Examples

# Generate sample data
n_obs <- 500
actual <- sample(0:1, n_obs, replace = TRUE, prob = c(0.7, 0.3))

# Generate slightly miscalibrated predictions based on actuals
predicted <- ifelse(actual == 1,
                    rbeta(n_obs, shape1 = 4, shape2 = 1.5),
                    rbeta(n_obs, shape1 = 1, shape2 = 4))
predicted <- pmin(pmax(predicted, 0), 1)

# Basic plot
calibration_plot(actual, predicted)


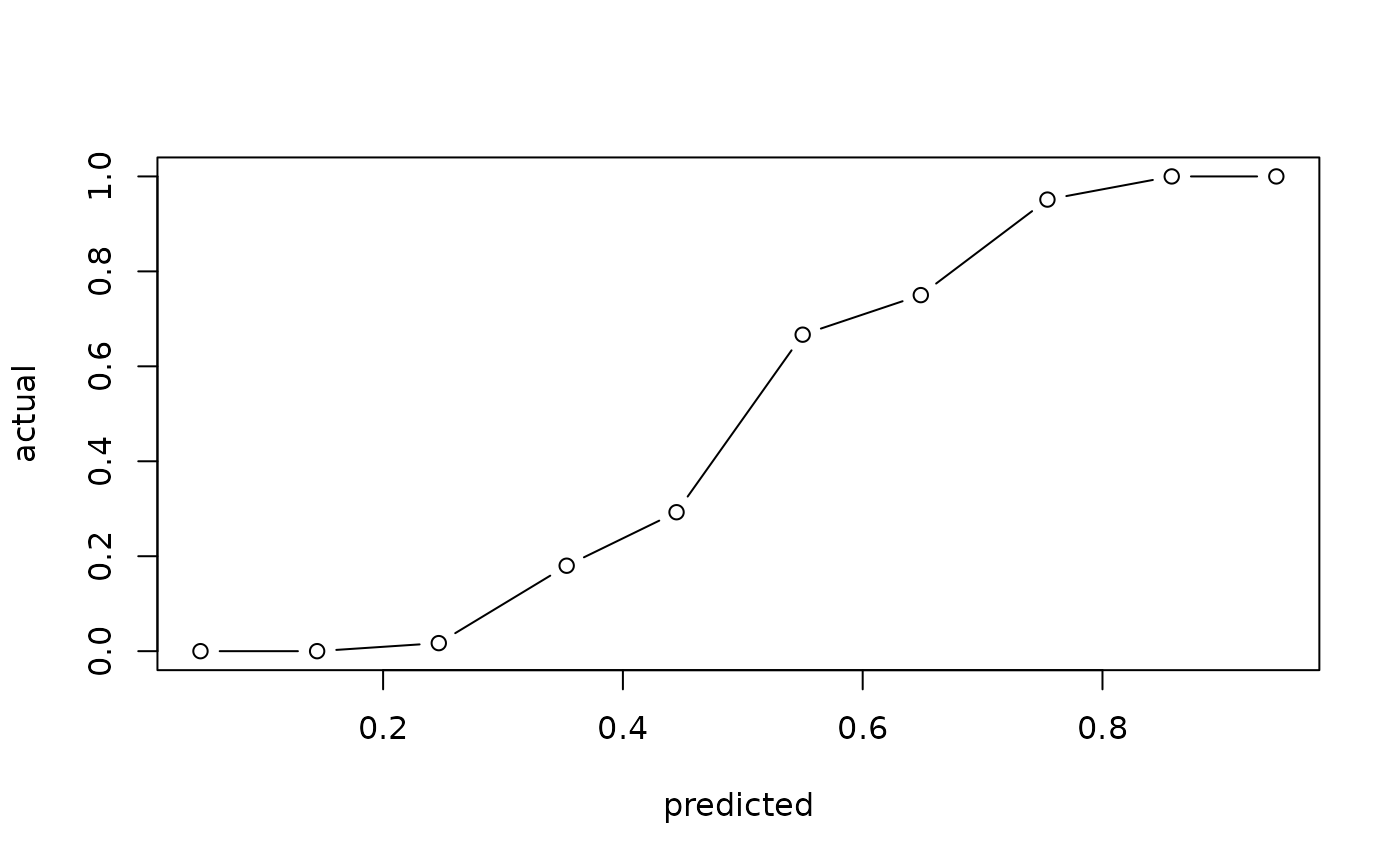# Customize the plot
calibration_plot(actual, predicted,
                 main = "Calibration Plot",
                 xlab = "Mean Predicted Probability",
                 ylab = "Observed Fraction of Positives",
                 col = "maroon",
                 pch = 19,
                 cex = 1.2)
 abline(0, 1, col = "gray50", lty = 2L)


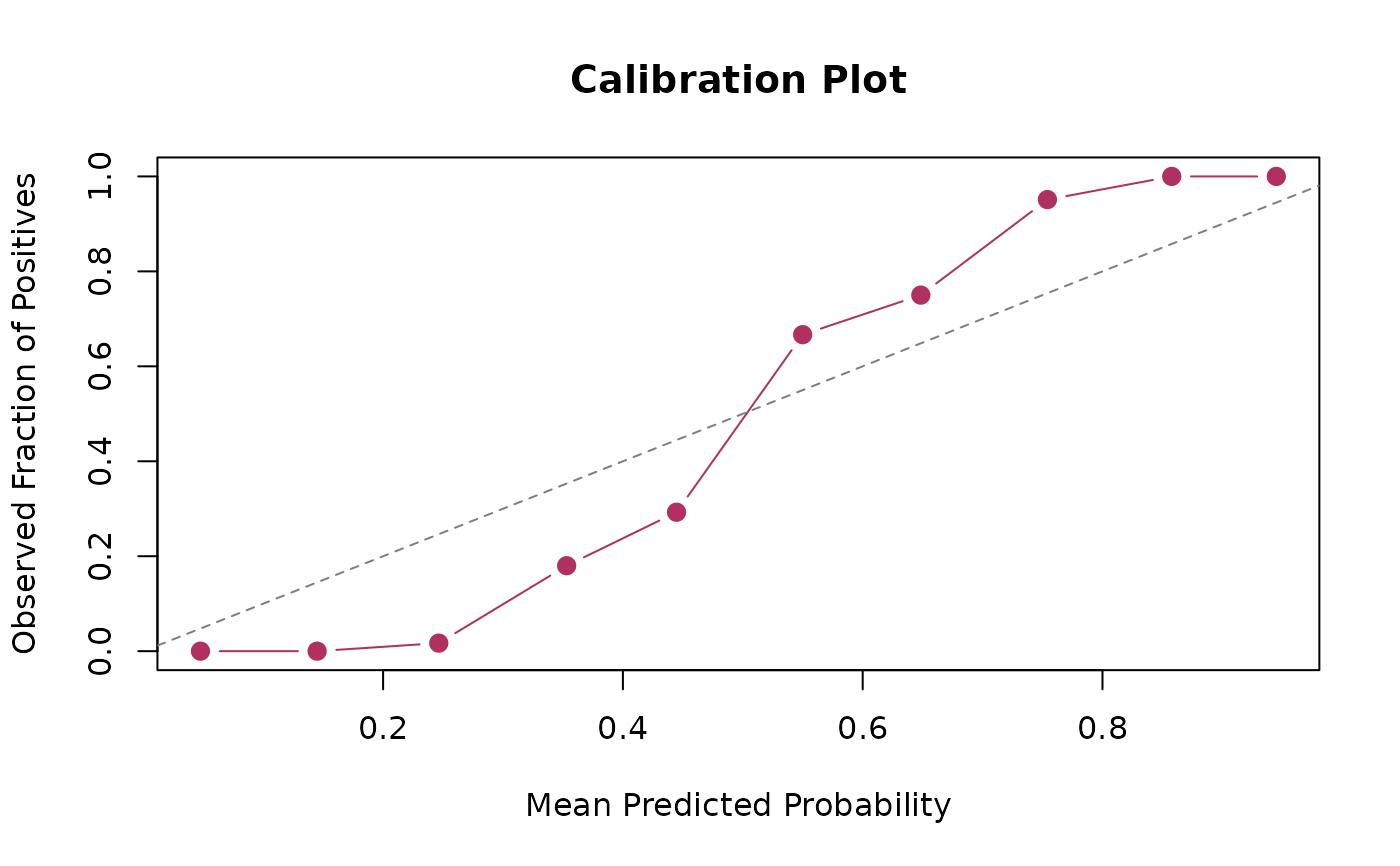# Get the summary data without plotting
cal_data <- calibration_plot(actual, predicted, show_plot = FALSE)
print(cal_data)
#> # A tibble: 10 × 4
#>      bin     n actual predicted
#>    <int> <int>  <dbl>     <dbl>
#>  1     1   104 0         0.0477
#>  2     2    89 0         0.145 
#>  3     3    59 0.0169    0.246 
#>  4     4    50 0.18      0.353 
#>  5     5    41 0.293     0.445 
#>  6     6    21 0.667     0.550 
#>  7     7    24 0.75      0.648 
#>  8     8    41 0.951     0.754 
#>  9     9    43 1         0.858 
#> 10    10    28 1         0.945