Skip to contents

Interpretation of Regression Models

Source: vignettes/articles/regression.Rmd
regression.Rmd

This article presents some examples of the interpretation of regression models using midr.

Regression Task

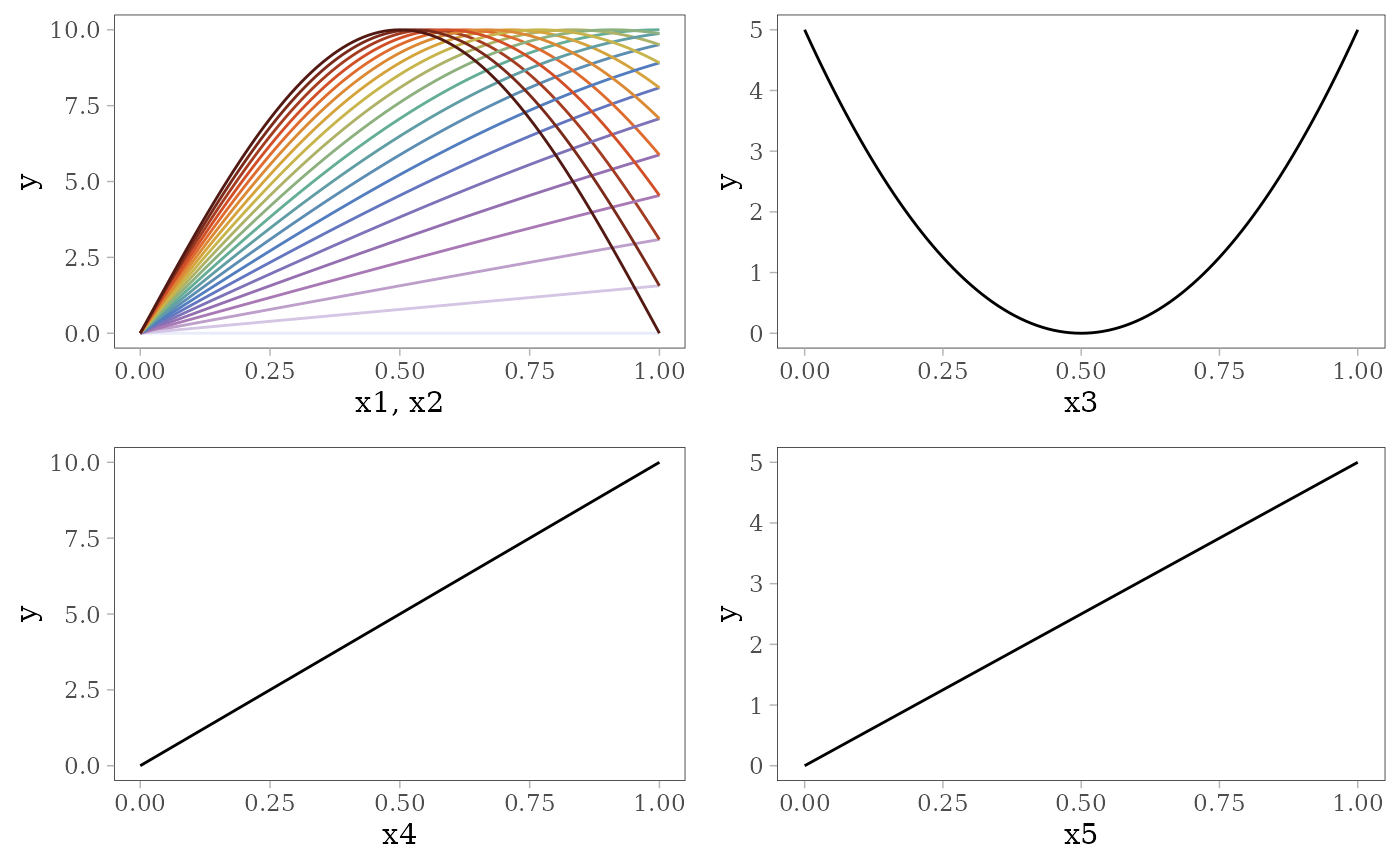
We use a benchmark regression task, originally described in Friedman (1991) and Breiman (1996), and implemented in the mlbench package. The dataset has 10 independent predictor variables x1,x2,...,x10x_1,x_2,...,x_{10} each uniformly distributed on the interval [0,1][0,1], and the response variable yy , generated according to the following formula with disturbance term ϵ∼𝒩(0,1)\epsilon\ {\sim}\ \mathcal{N}{(0, 1)}. y=10sin(πx1x2)+20(x3−0.5)2+10x4+5x5+ϵ y=10\sin{(\pi{x_1}{x_2})+20{(x_3-0.5)}^2+10x_4+5x_5+\epsilon}

The following plots show the effect of each predictor variable on the response. For x1x_1 and x2x_2 , the interaction effect is shown by the colored lines: the effect of x1x_1 depends on the value of x2x_2 (pale purple for 0 and dark red for 1) and vice versa.

# benchmark regression task
library(mlbench)
set.seed(42)
train  <- as.data.frame(mlbench.friedman1(n = 500L))
test   <- as.data.frame(mlbench.friedman1(n = 500L))
mtrain <- as.data.frame(mlbench.friedman1(n = 2500L))[, -11L]

For each model type, we fit a regression model using the train data of 500 observations and an interpretative MID surrogate of the target model using the mtrain data of 2500 observations without the response variable. We then evaluate the predictive accuracy of the target model and the interpretative accuracy of the MID surrogate based on the RMSE between the test and model prediction or the two predictions, respectively.

# define utility functions for the following chunks
effect_plots <- function(object) {
  mid.plots(object, terms = paste("x", 1:6, sep = "."))
}

interaction_plot <- function(object) {
  ggmid(object, "x.1:x.2", main.effects = TRUE, theme = "sunset") +
    ggtitle("interaction effect")
}

ice_theme <- color.theme("mako")
ice_plot <- function(object, data = train[1:200, ]) {
  ggmid(mid.conditional(object, "x.1", data = data),
        var.color = x.2, type = "centered", theme = ice_theme) +
    ggtitle("conditional expectation")
}

importance_plot <- function(object) {
  ggmid(mid.importance(object), "heatmap") +
    ggtitle("feature importance")
}

eval_plot <- function(model, mid, data = test, ...) {
  pred <- get.yhat(model, data, ...)
  pred_mid <- get.yhat(mid, data)
  actual <- test$y
  rmse_vs_test <- rmse(pred, actual)
  rmse_vs_mid <-  rmse(pred, pred_mid)
  ggplot() + scale_color_theme("highlight?accent='steelblue'") +
    geom_point(aes(x = pred, y = actual, col = "vs test")) +
    geom_point(aes(x = pred, y = pred_mid, col = "vs mid")) +
    geom_abline(slope = 1, intercept = 0, col = "black", lty = 2) +
    labs(x = "model-prediction", y = "mid-prediction / test") +
    annotate(
      "text", family = "serif", size = 3,
      x = min(pred) + diff(range(pred)) / 8,
      y = max(actual) - diff(range(actual) / 8),
      label = sprintf("RMSE\nvs test: %.3f\nvs mid: %.3f",
                      rmse_vs_test, rmse_vs_mid)
    ) + ggtitle("prediction / representation accuracy")
}
ml <- midlist()

Additive Models

Linear Model 

model <- lm(y ~ ., train)
coef(model)
#> (Intercept)         x.1         x.2         x.3         x.4         x.5 
#>   0.1302510   6.8458545   6.8892805  -0.4403955  10.3264576   4.6735425 
#>         x.6         x.7         x.8         x.9        x.10 
#>   0.5837944   0.2030152  -0.6272202  -0.1722106   0.3453933
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: lm
#> 
#> Intercept: 14.319
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0
grid.arrange(grobs = effect_plots(mid), nrow = 2L)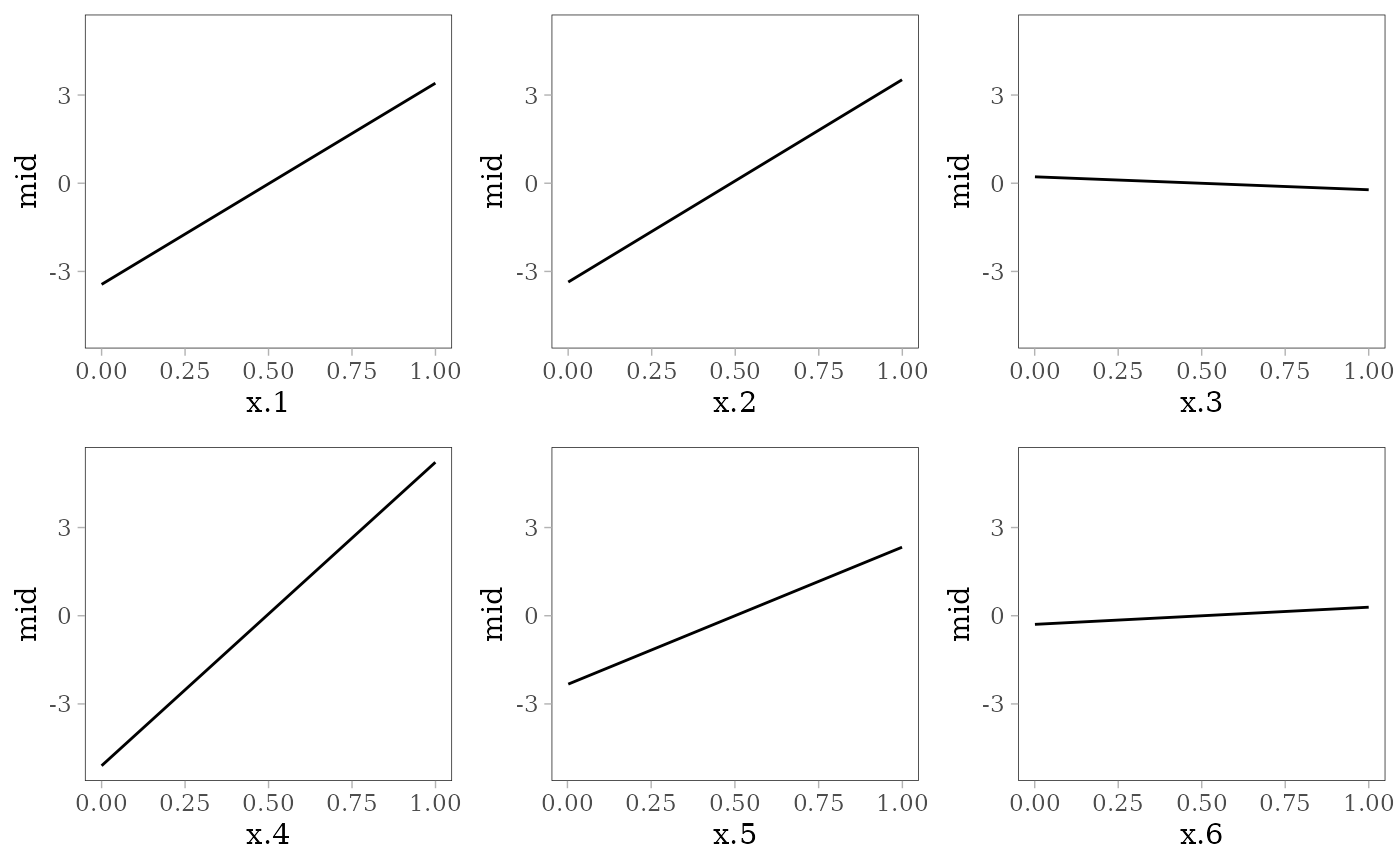

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)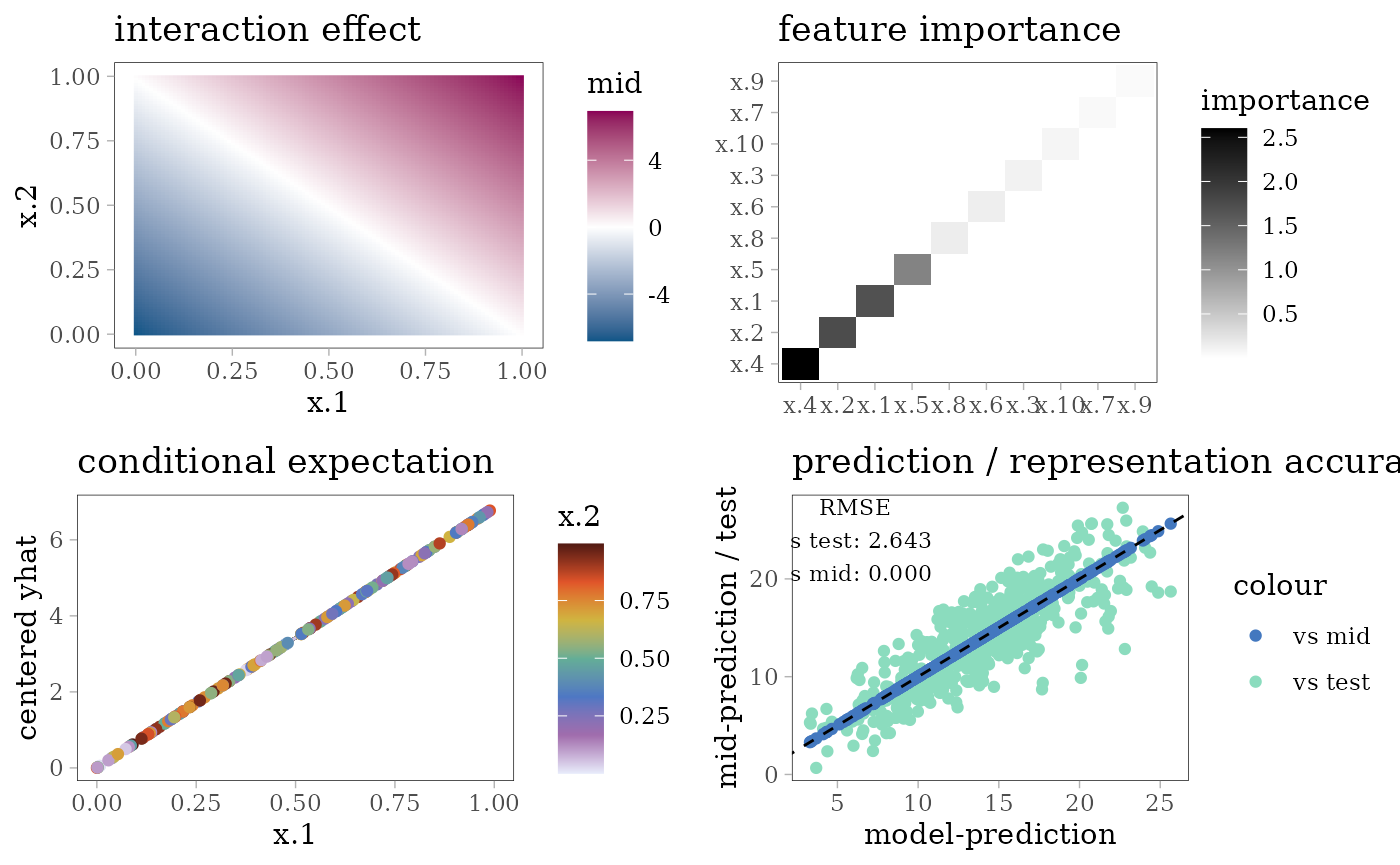

ml$lm <- mid

Regularized GLM 

library(glmnet)
model <- glmnet(x = as.matrix(train[, -11]), y = train[, 11])
# prediction with arbitrarily chosen lambda
mid <- interpret(y ~ .^2, mtrain[, -11], model,
                 pred.args = list(s = model$lambda[9]))
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain[, -11], model = model,
#>  pred.args = list(s = model$lambda[9]))
#> 
#> Model Class: elnet, glmnet
#> 
#> Intercept: 14.374
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0
grid.arrange(grobs = effect_plots(mid), nrow = 2L)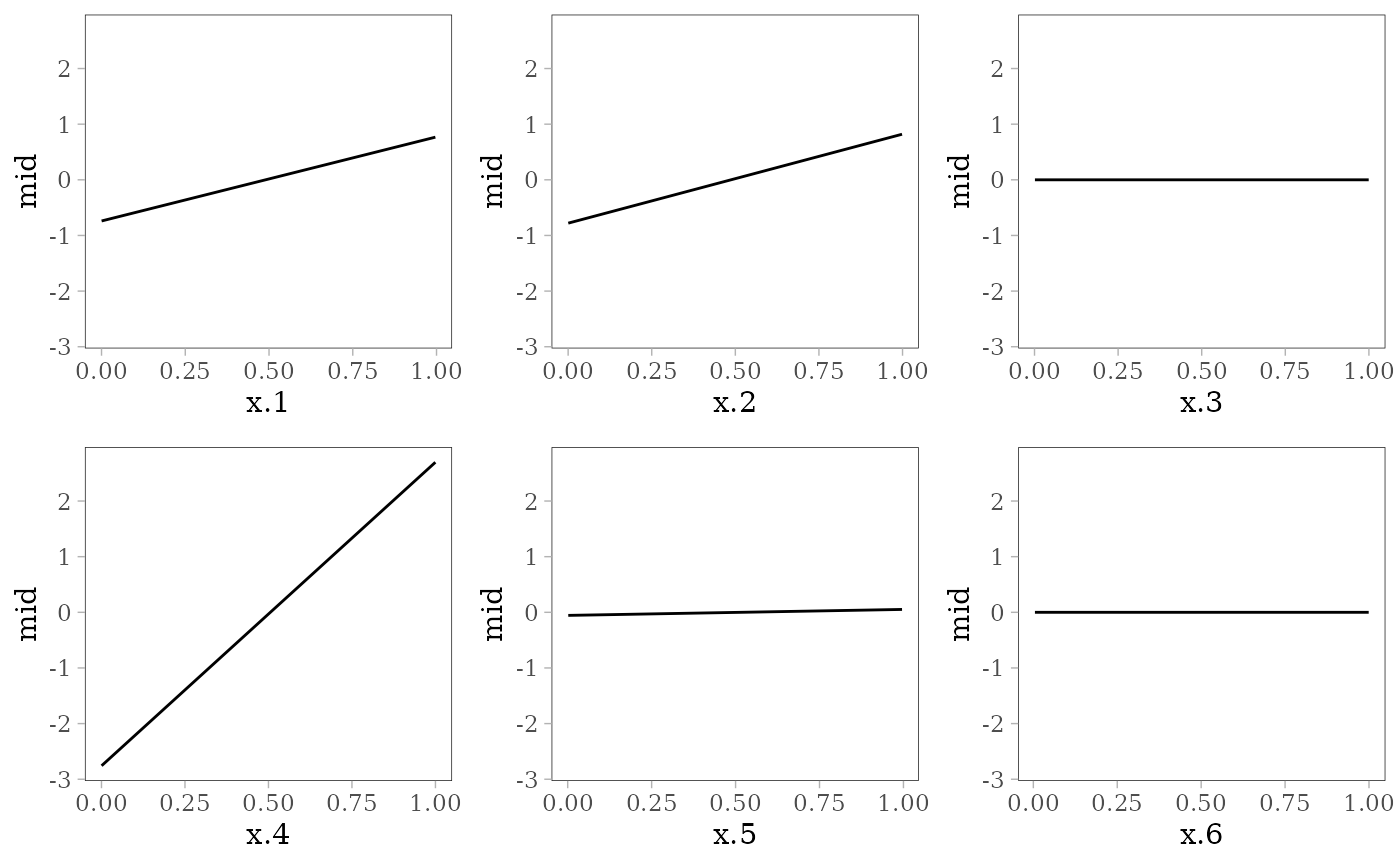

evp <- eval_plot(model, mid, data = test[, -11],
                       s = model$lambda[9])
grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), evp, nrow = 2)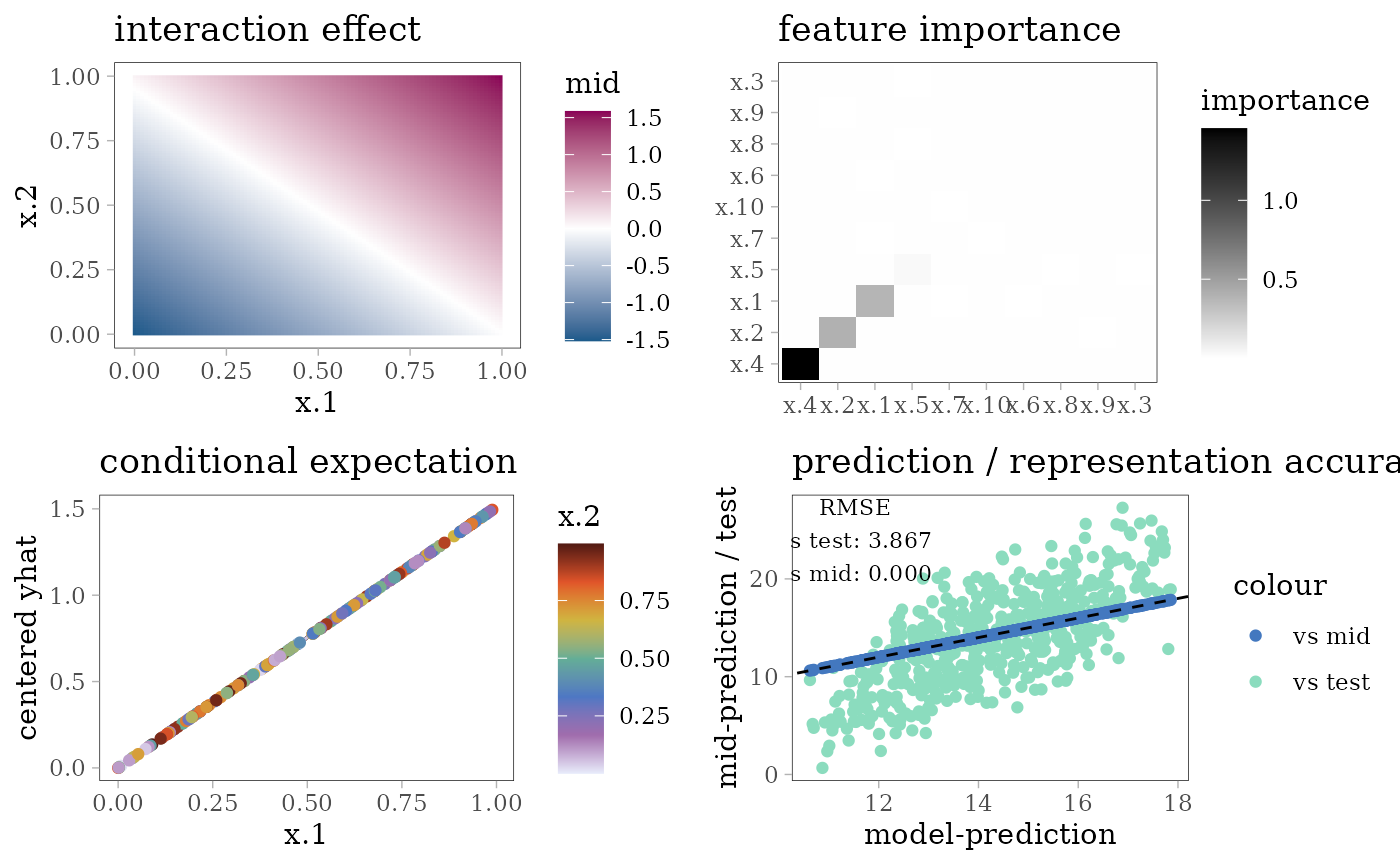

Generalized Additive Model 

library(gam)
model <- gam(y ~ s(x.1) + s(x.2) + s(x.3) + s(x.4) + s(x.5) +
             s(x.6) + s(x.7) + s(x.8) + s(x.9) + s(x.10),
             family = gaussian, data = train)
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: Gam, glm, lm
#> 
#> Intercept: 14.323
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 3.9583e-07
grid.arrange(grobs = effect_plots(mid), nrow = 2L)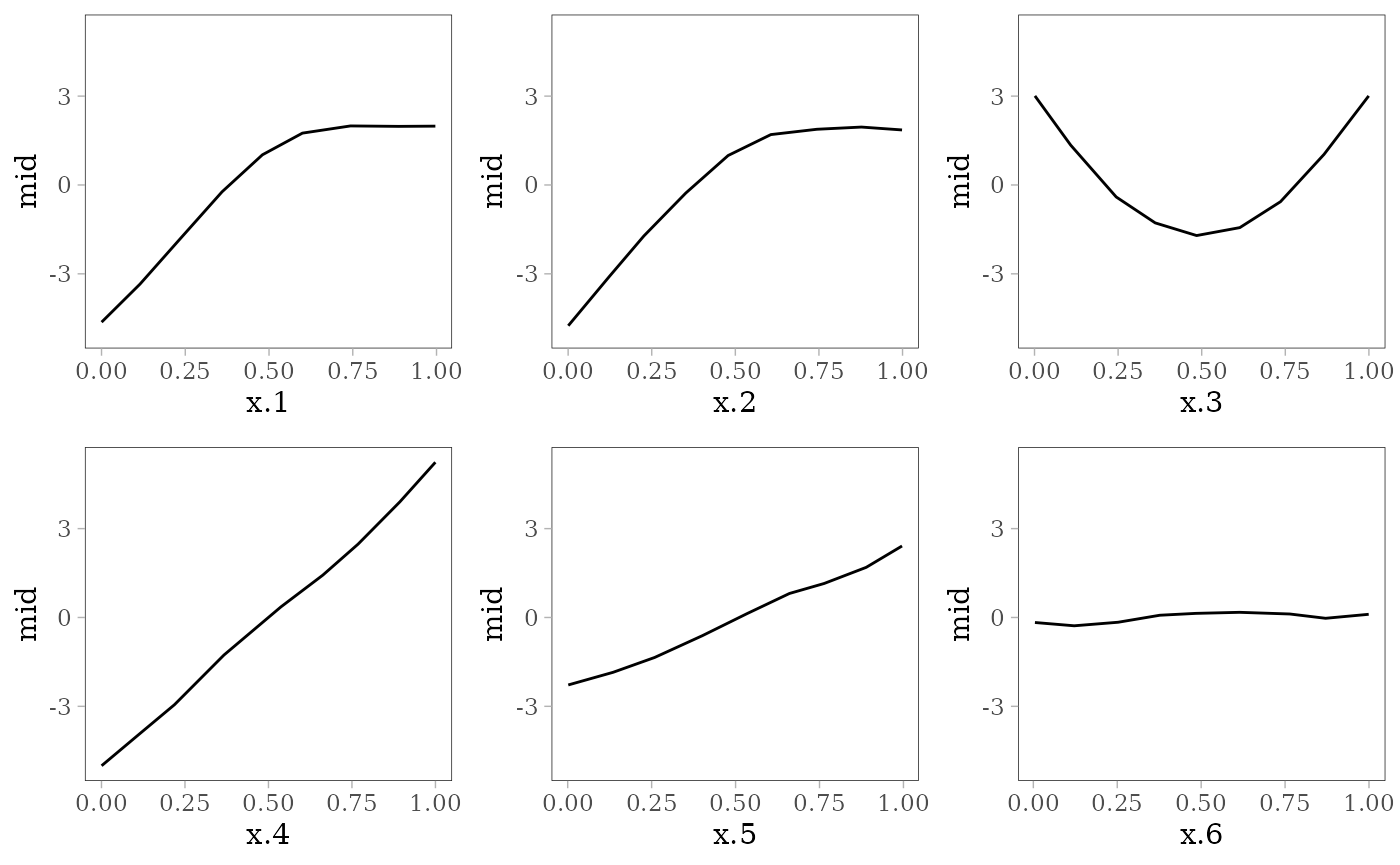

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)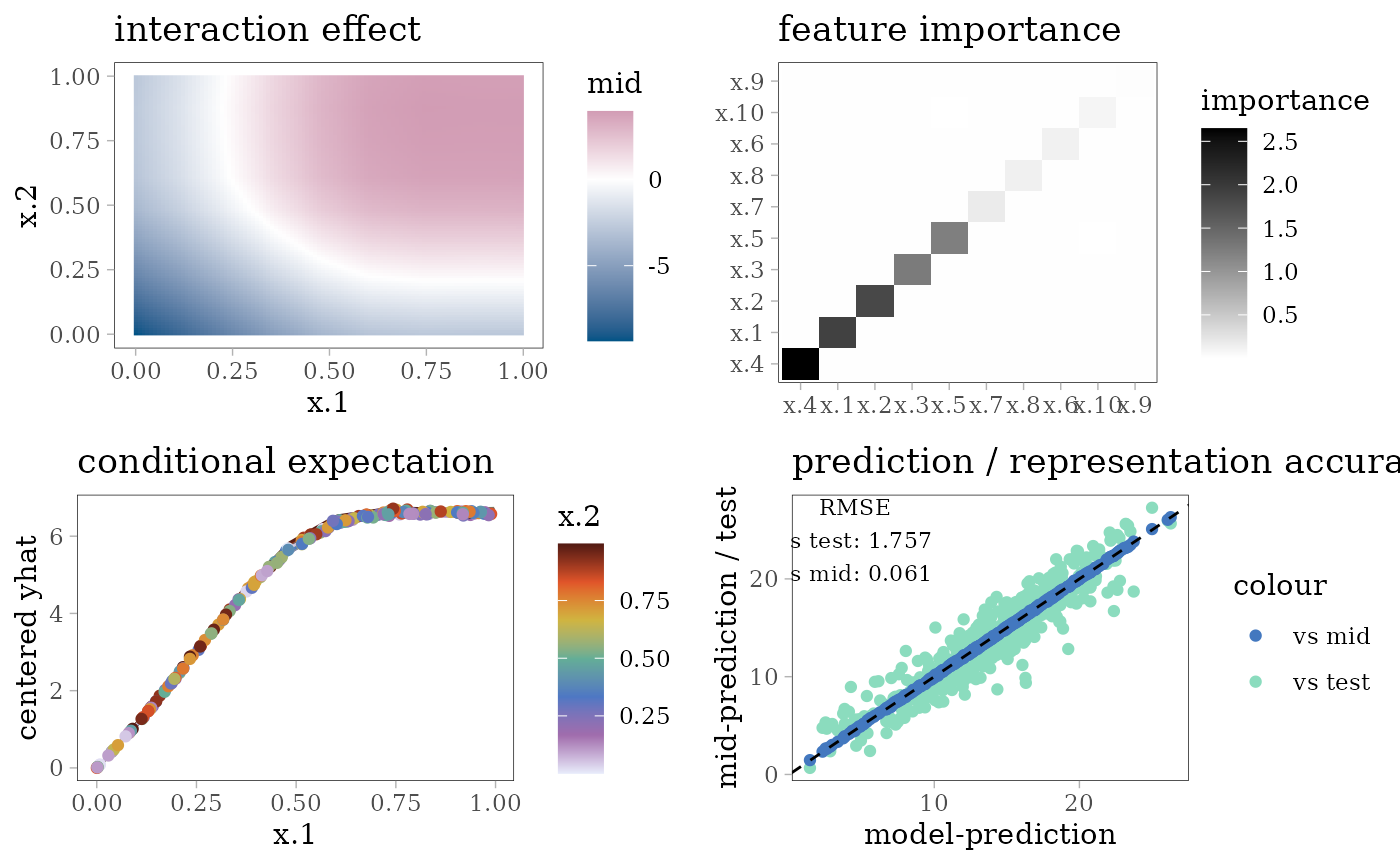

ml$gam <- mid

Multivariate Adaptive Regression Spline 

library(earth)
model <- earth(y ~ ., degree = 2, data = train)
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: earth
#> 
#> Intercept: 14.182
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.00051402
grid.arrange(grobs = effect_plots(mid), nrow = 2L)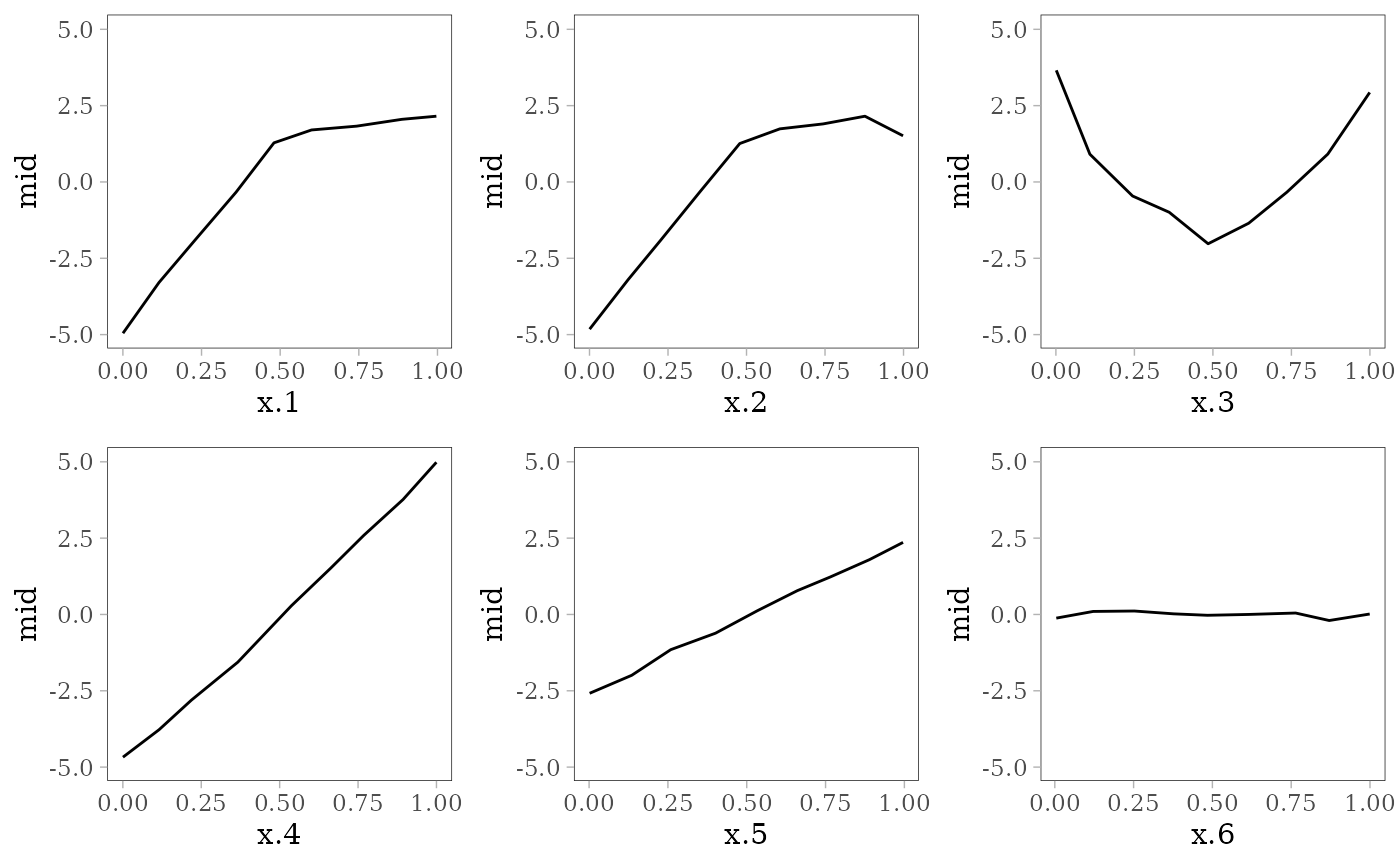

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)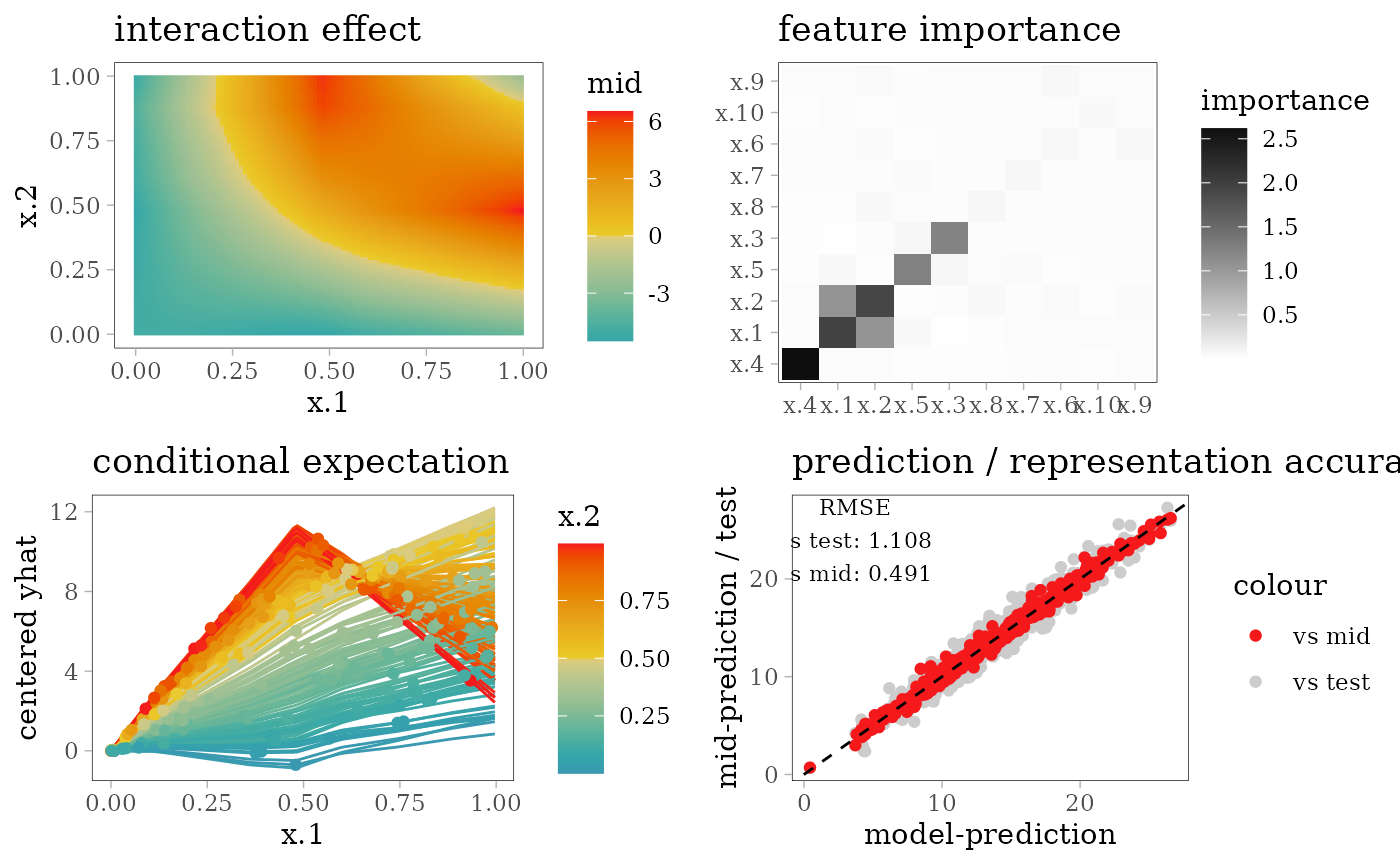

ml$mars <- mid

Neural Network

Single Hidden Layer Network 

library(nnet)
set.seed(42)
model <- nnet(y ~ ., train, size = 5, linout = TRUE, maxit = 1e3, trace = FALSE)
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: nnet.formula, nnet
#> 
#> Intercept: 14.195
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.00281
grid.arrange(grobs = effect_plots(mid), nrow = 2L)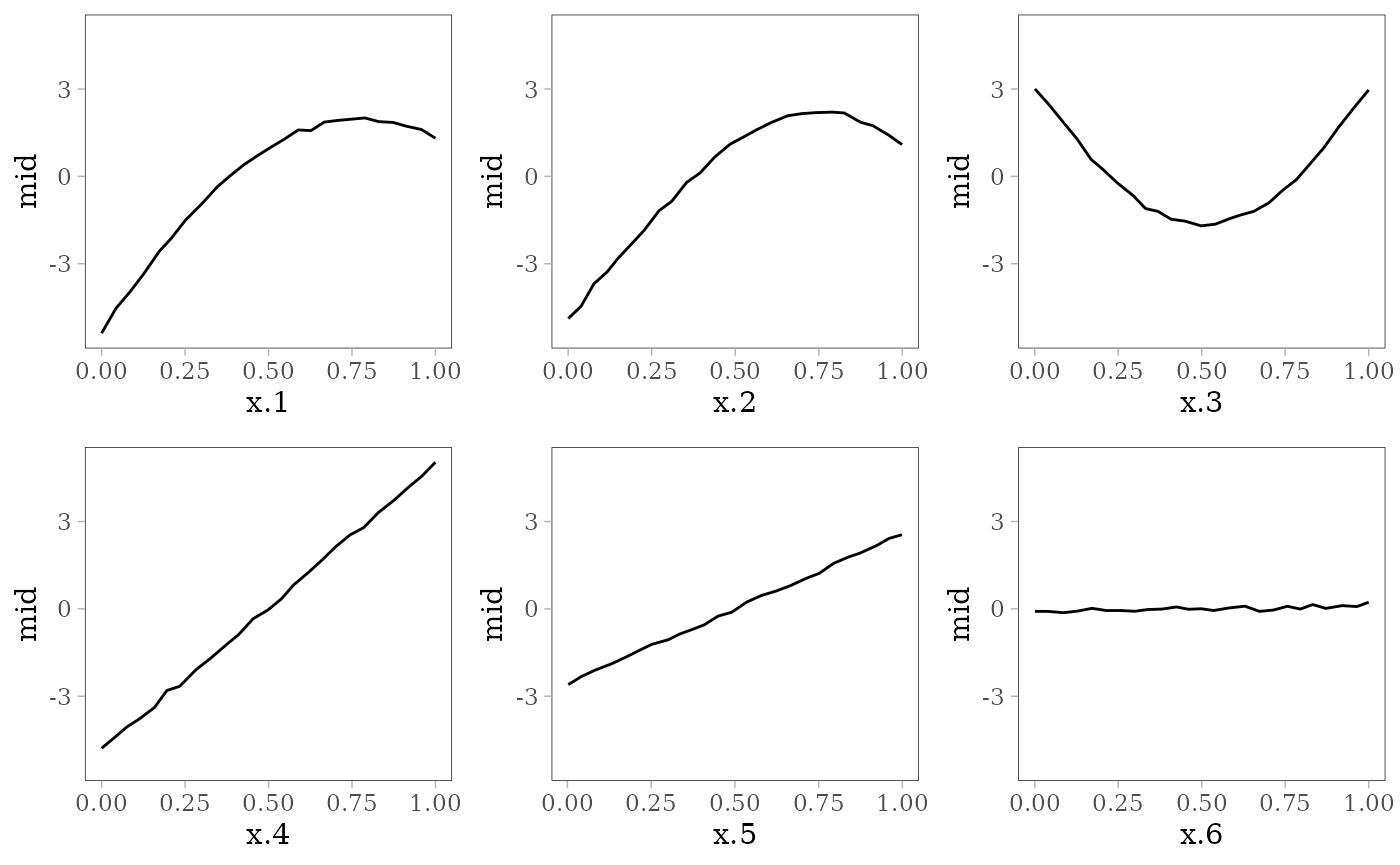

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)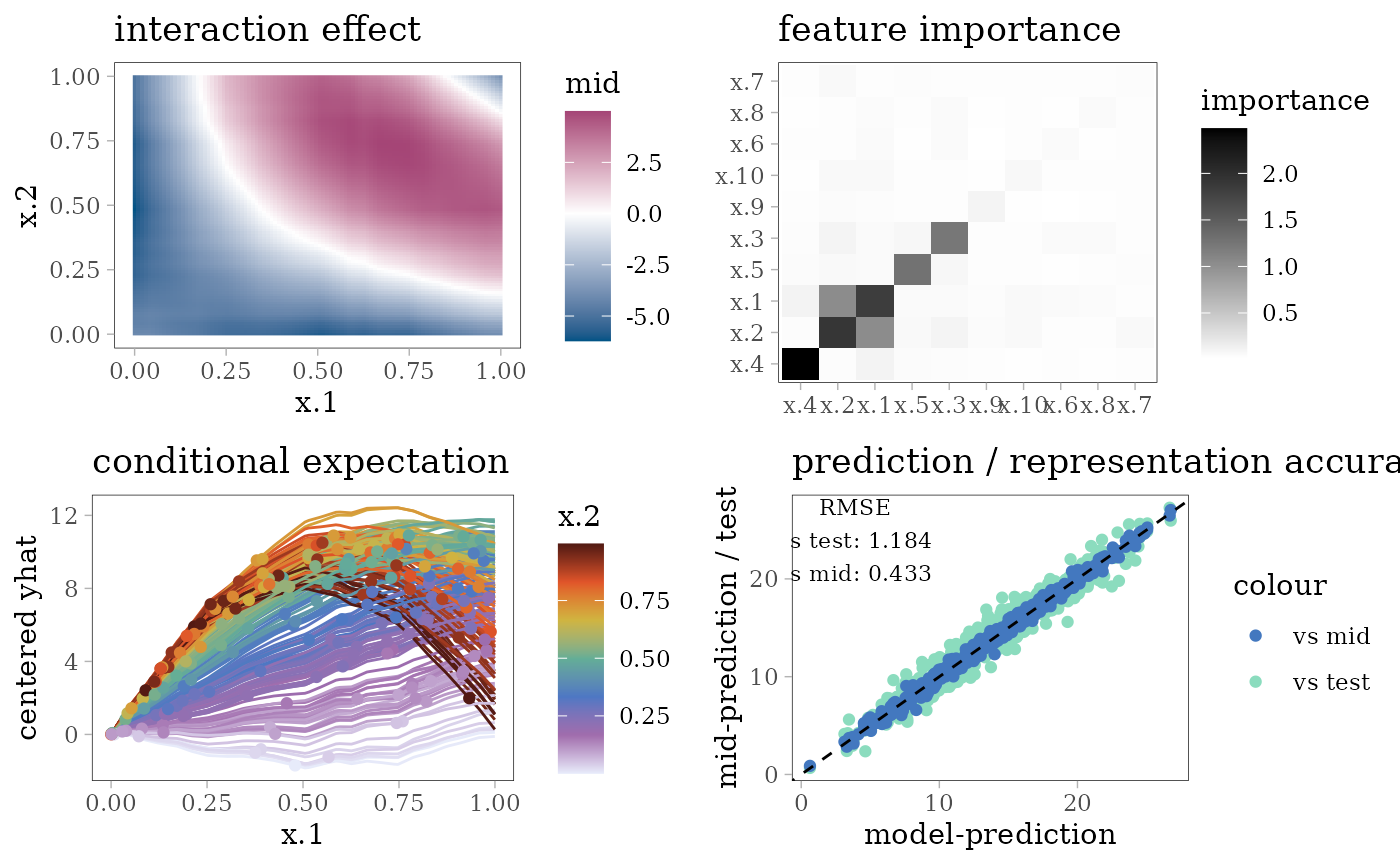

ml$nnet <- mid

Support Vector Machine

RBF Kernel SVM 

library(e1071)
#> 
#> Attaching package: 'e1071'
#> The following object is masked from 'package:ggplot2':
#> 
#>     element
model <- svm(y ~ ., train, kernel = "radial")
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: svm.formula, svm
#> 
#> Intercept: 14.32
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.0075534
grid.arrange(grobs = effect_plots(mid), nrow = 2L)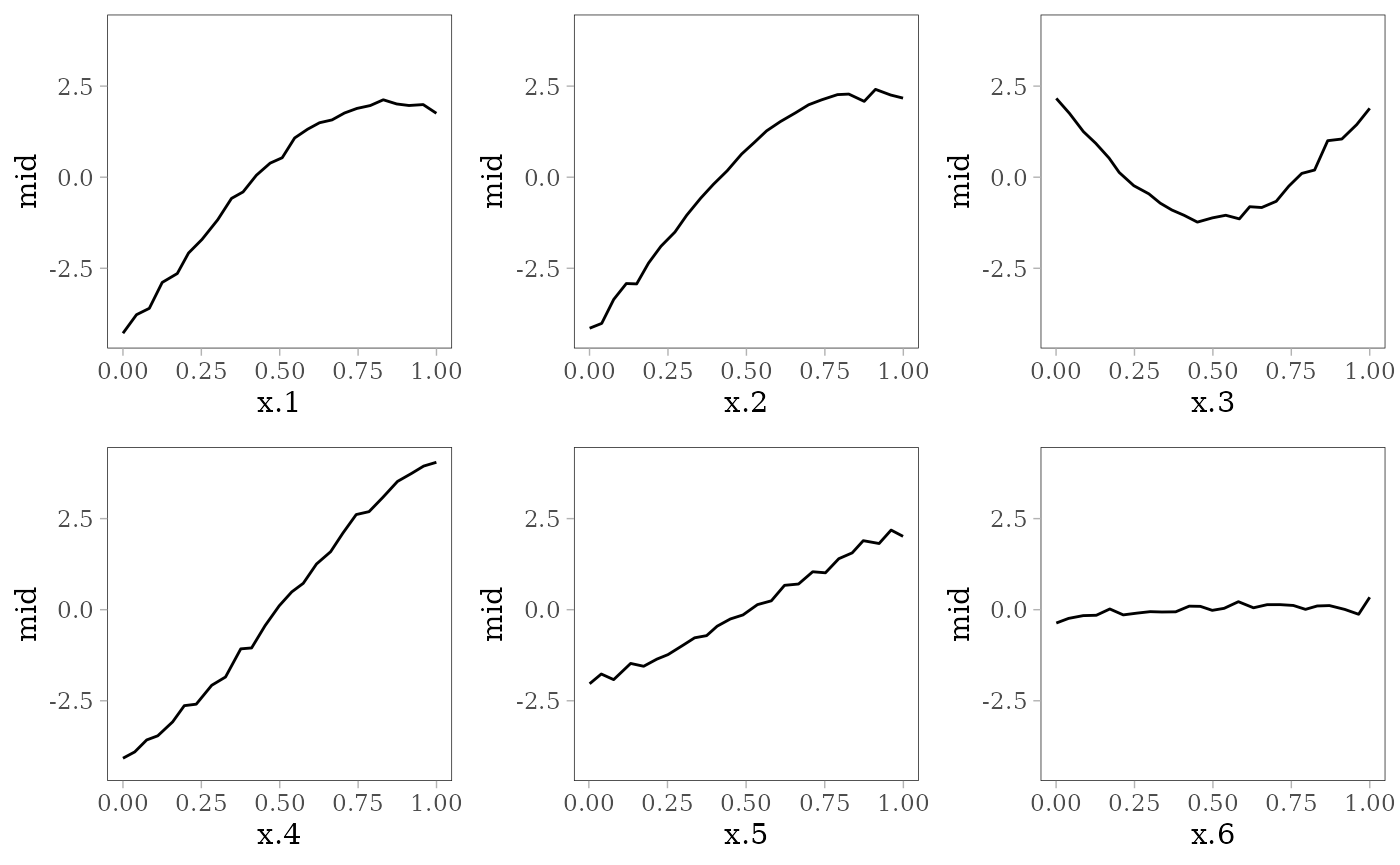

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)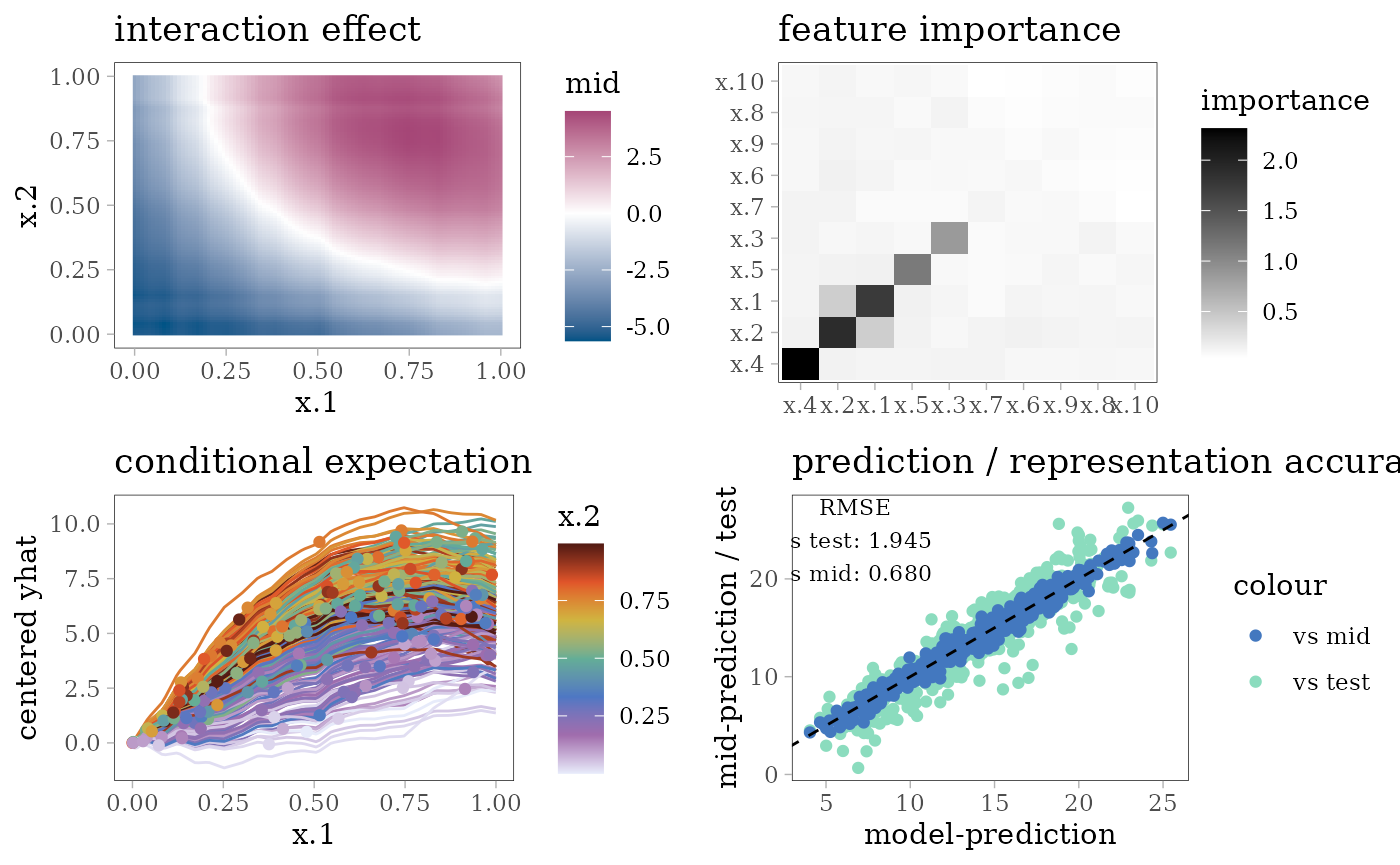

ml$svm <- mid

Tree Based Models

Gradient Boosting Trees 

library(xgboost)
params <- list(eta = .1, subsample = .7, max_depth = 5)
set.seed(42)
model <- xgboost(as.matrix(train[, -11]), train[, 11], nrounds = 100,
                 params = params, verbose = 0)
#> Warning in throw_err_or_depr_msg("Parameter(s) have been removed from this
#> function: ", : Parameter(s) have been removed from this function: params. This
#> warning will become an error in a future version.
#> Warning in throw_err_or_depr_msg("Passed unrecognized parameters: ",
#> paste(head(names_unrecognized), : Passed unrecognized parameters: verbose. This
#> warning will become an error in a future version.
mid <- interpret(y ~ .^2, as.matrix(mtrain), model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = as.matrix(mtrain), model = model)
#> 
#> Model Class: xgboost, xgb.Booster
#> 
#> Intercept: 14.307
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.030268
grid.arrange(grobs = effect_plots(mid), nrow = 2L)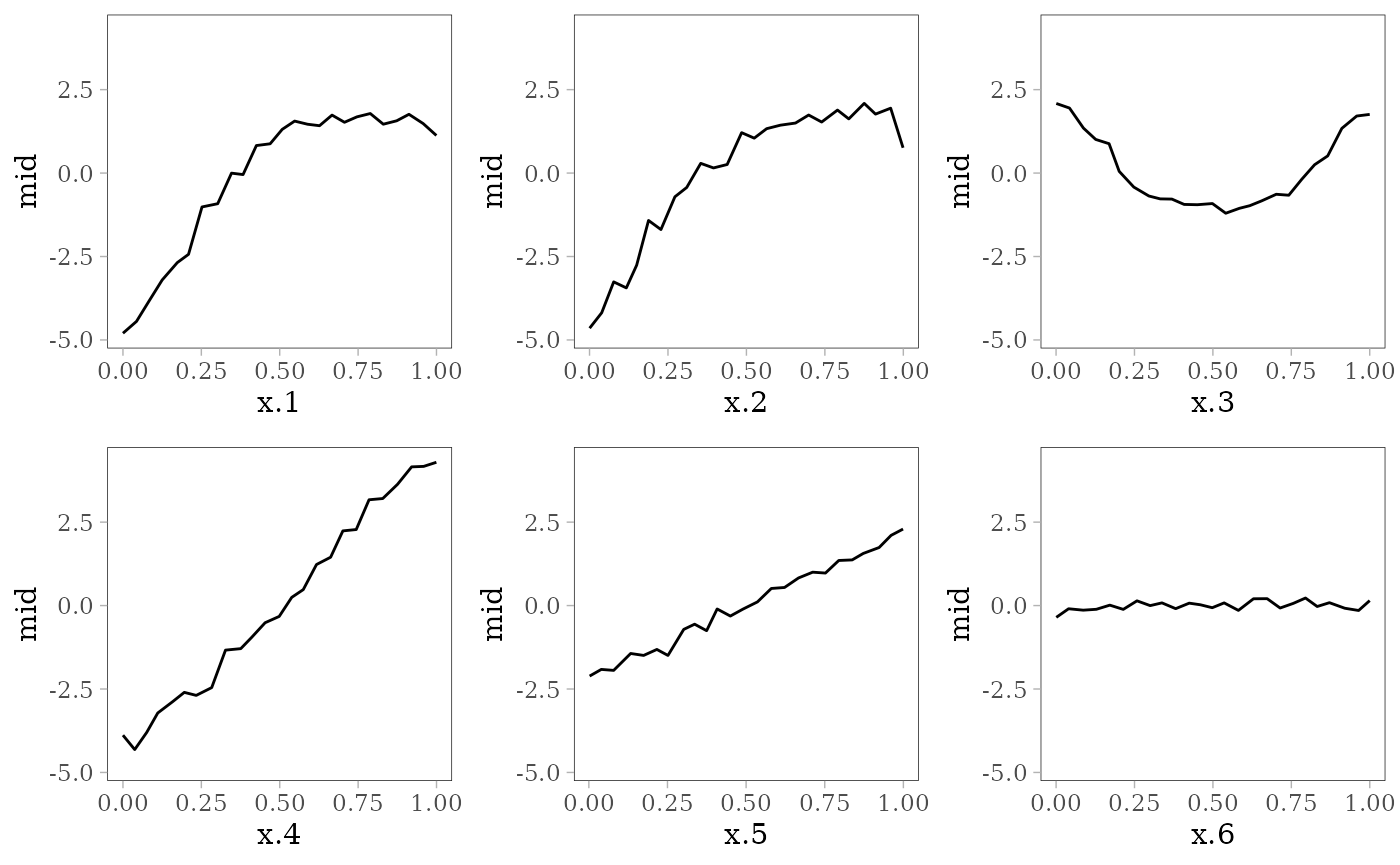

evp <- eval_plot(model, mid, as.matrix(test[, -11]))
grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), evp, nrow = 2)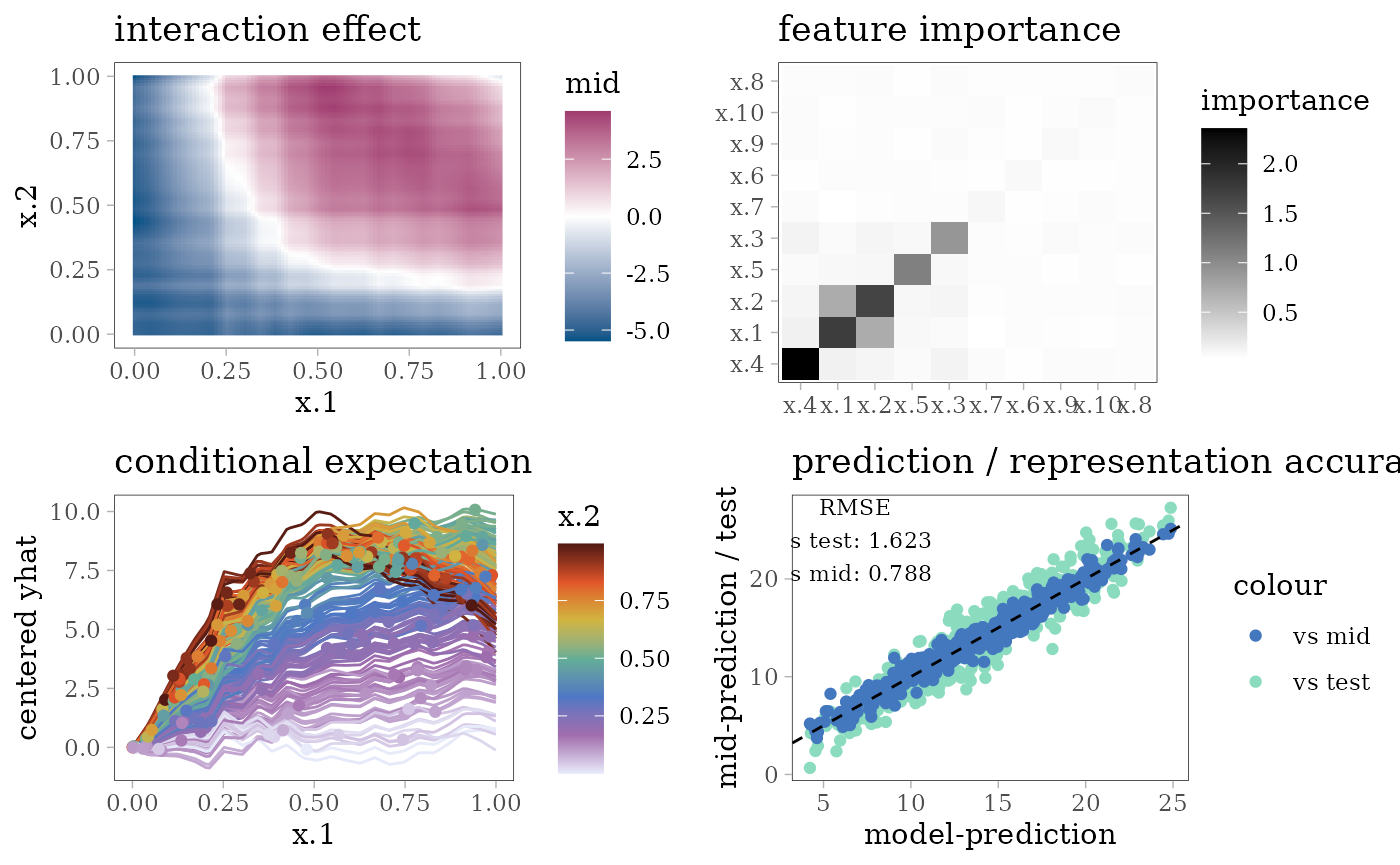

ml$xgb <- mid

Random Forest 

library(ranger)
set.seed(42)
model <- ranger(y ~ ., train, mtry = 5)
mid <- interpret(y ~ .^2, mtrain, model)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model)
#> 
#> Model Class: ranger
#> 
#> Intercept: 14.27
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.0075659
grid.arrange(grobs = effect_plots(mid), nrow = 2L)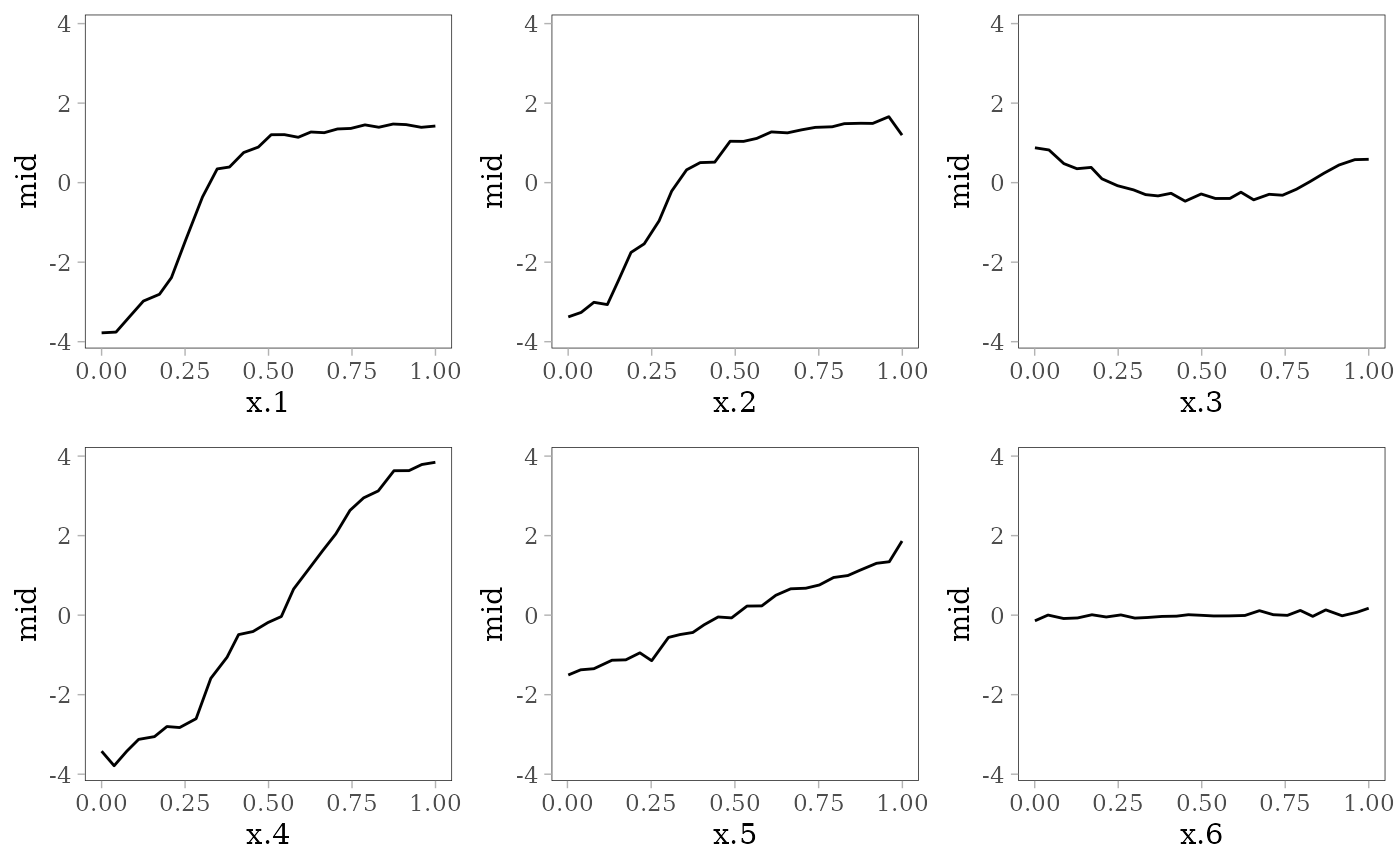

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)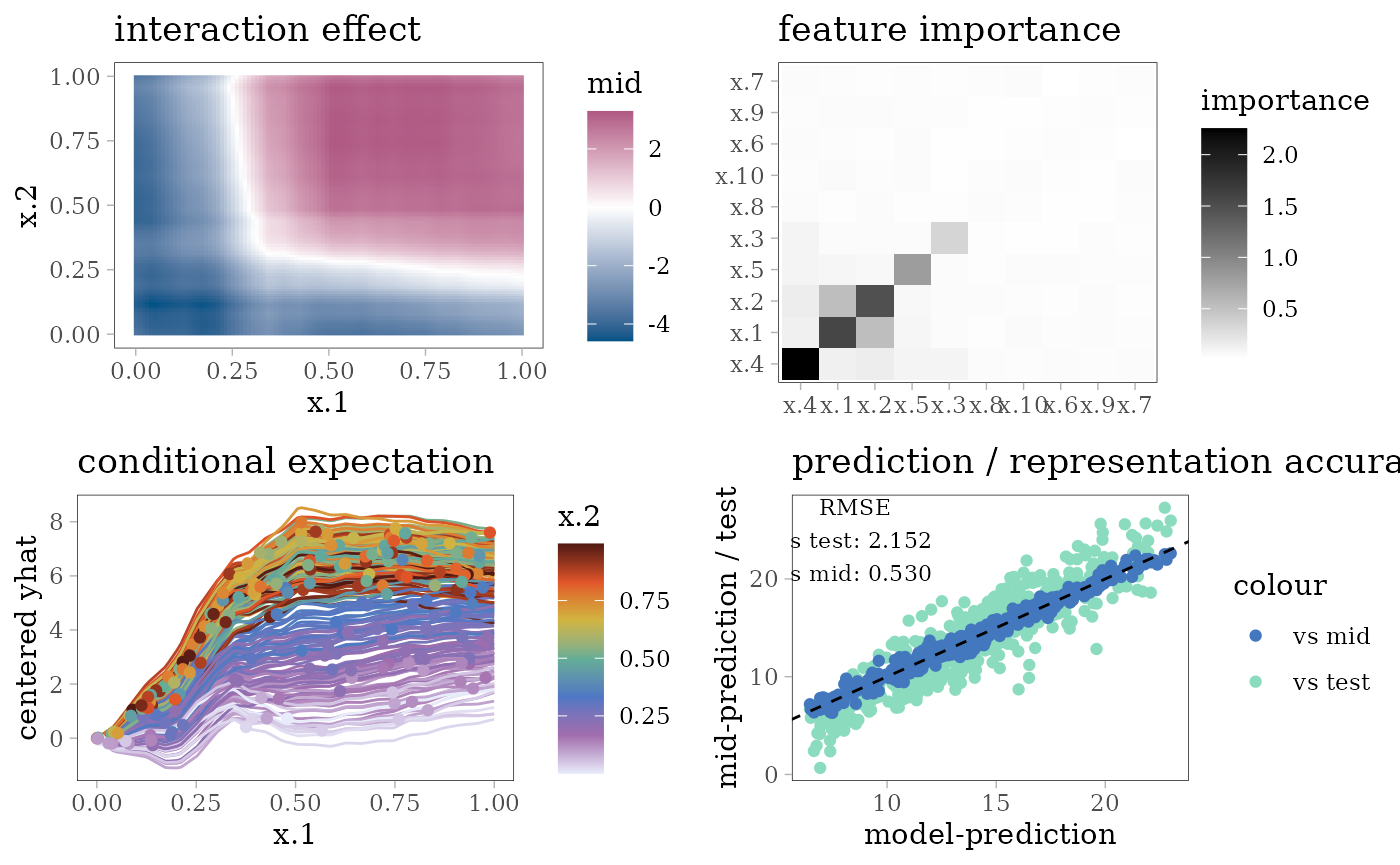

ml$rf <- mid

Decision Tree 

library(rpart)
model <- rpart(y ~ ., train)
# create encoding frames for CART
frm <- cbind(model$frame, labels(model, collapse = FALSE))
print(t(frm[frm$var != "<leaf>", c("var", "ltemp")]))
#>       1          2        5         11         22         3          7         
#> var   "x.4"      "x.1"    "x.2"     "x.4"      "x.5"      "x.2"      "x.1"     
#> ltemp "< 0.5579" "< 0.21" "< 0.311" "< 0.2953" "< 0.5849" "< 0.2653" "< 0.3184"
#>       14         15         31         62        
#> var   "x.4"      "x.5"      "x.4"      "x.2"     
#> ltemp "< 0.8843" "< 0.2486" "< 0.8413" "< 0.4782"
frames <- lapply(mtrain, range)
frames$x.1 <- c(frames$x.1, .2100, .3184)
frames$x.2 <- c(frames$x.2, .3110, .2653, .4782)
frames$x.4 <- c(frames$x.4, .5579, .2953, .8843, .8413)
frames$x.5 <- c(frames$x.5, .5849, .2486)
mid <- interpret(y ~ .^2, mtrain, model, type = 0, frames = frames)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = mtrain, model = model, type = 0,
#>  frames = frames)
#> 
#> Model Class: rpart
#> 
#> Intercept: 14.264
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.031256
grid.arrange(grobs = effect_plots(mid), nrow = 2L)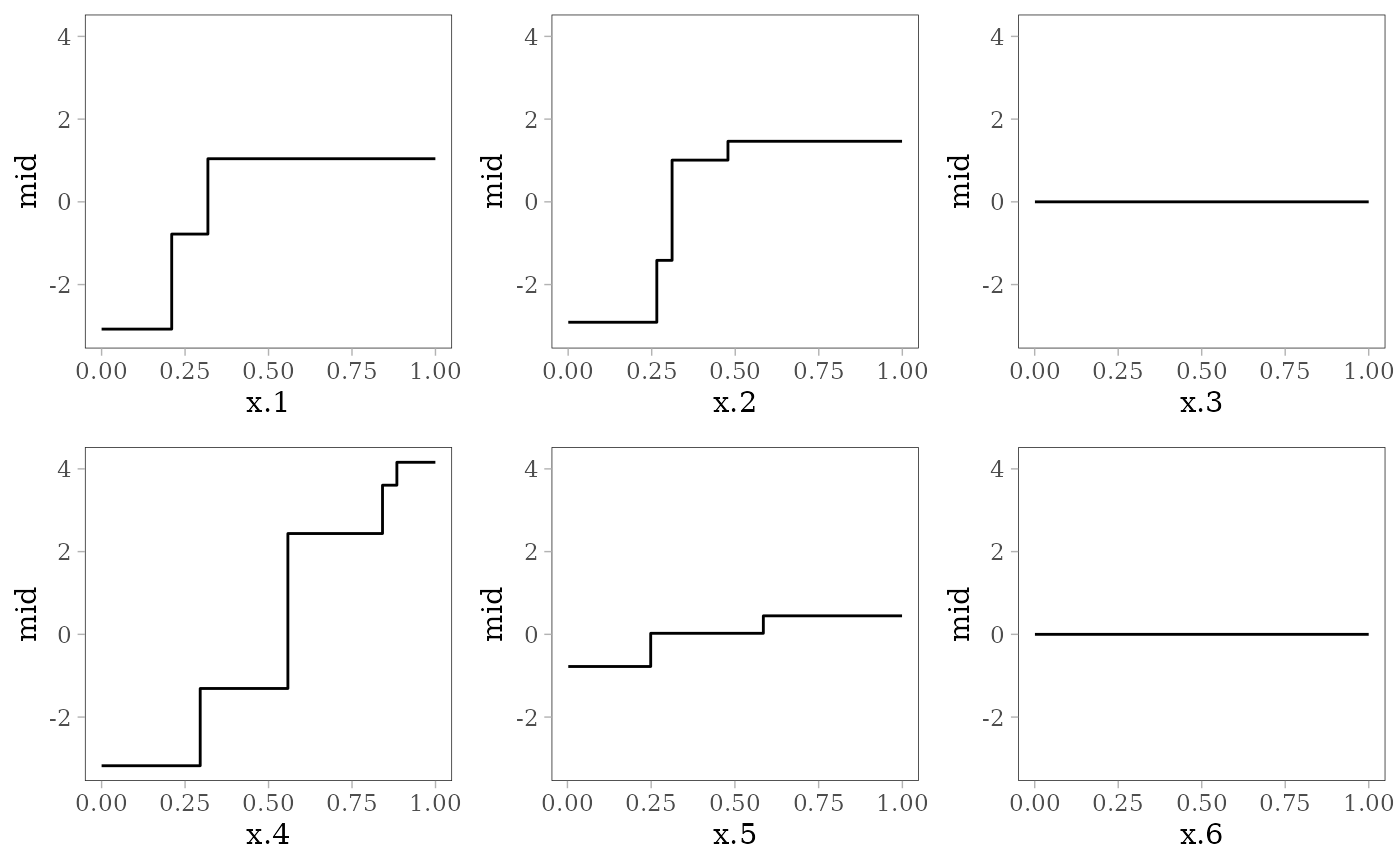

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)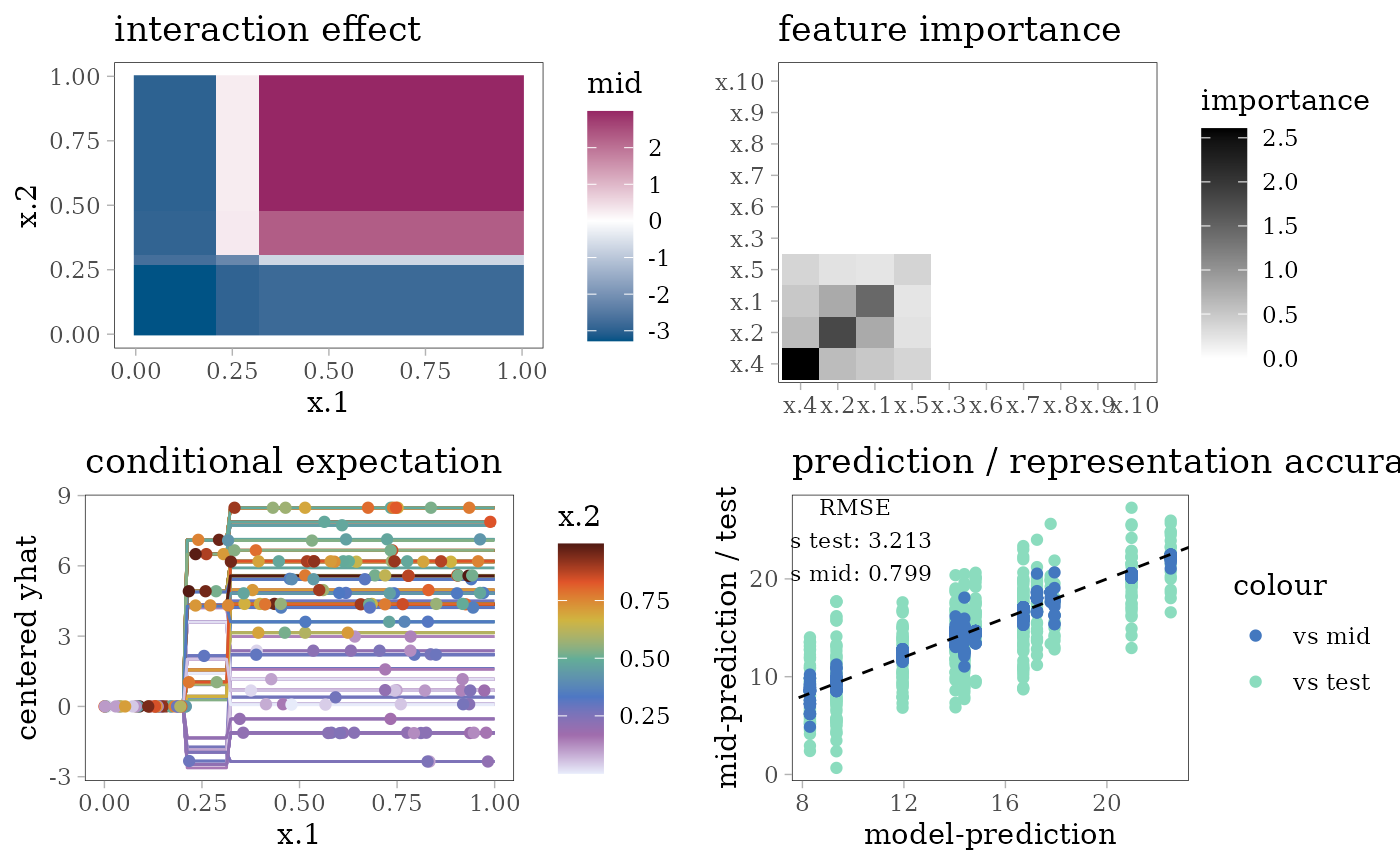

ml$tree <- mid

Other Modes

Predictive MID 

model <- mid <- interpret(y ~ .^2, train, lambda = .2)
#> 'model' not passed: response variable in 'data' is used
pred <- pred_mid <- predict(mid, test)
print(mid)
#> 
#> Call:
#> interpret(formula = y ~ .^2, data = train, lambda = 0.2)
#> 
#> Intercept: 14.417
#> 
#> Main Effects:
#> 10 main effect terms
#> 
#> Interactions:
#> 45 interaction terms
#> 
#> Uninterpreted Variation Ratio: 0.03179
grid.arrange(grobs = effect_plots(mid), nrow = 2L)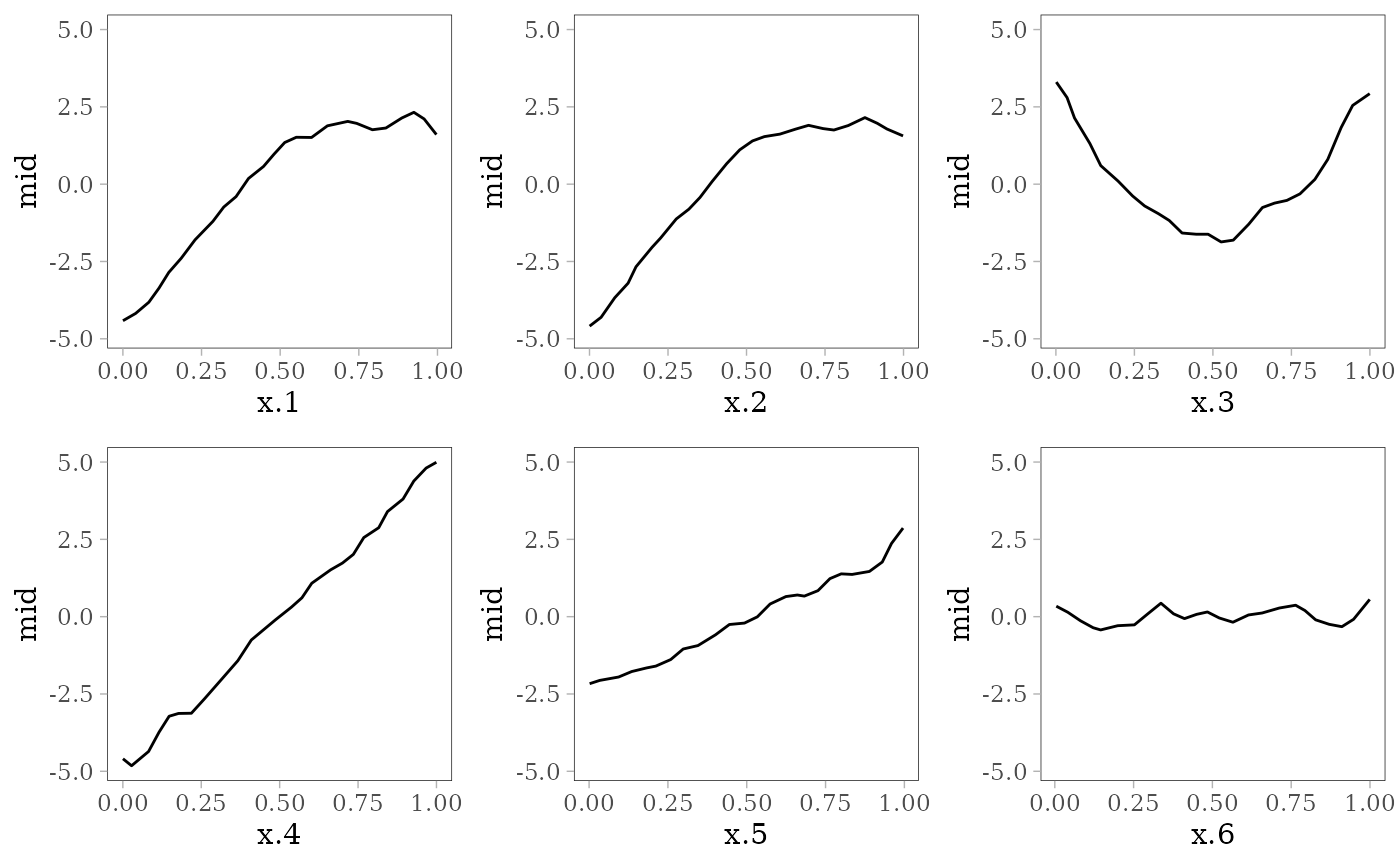

grid.arrange(interaction_plot(mid), importance_plot(mid),
             ice_plot(mid), eval_plot(model, mid), nrow = 2)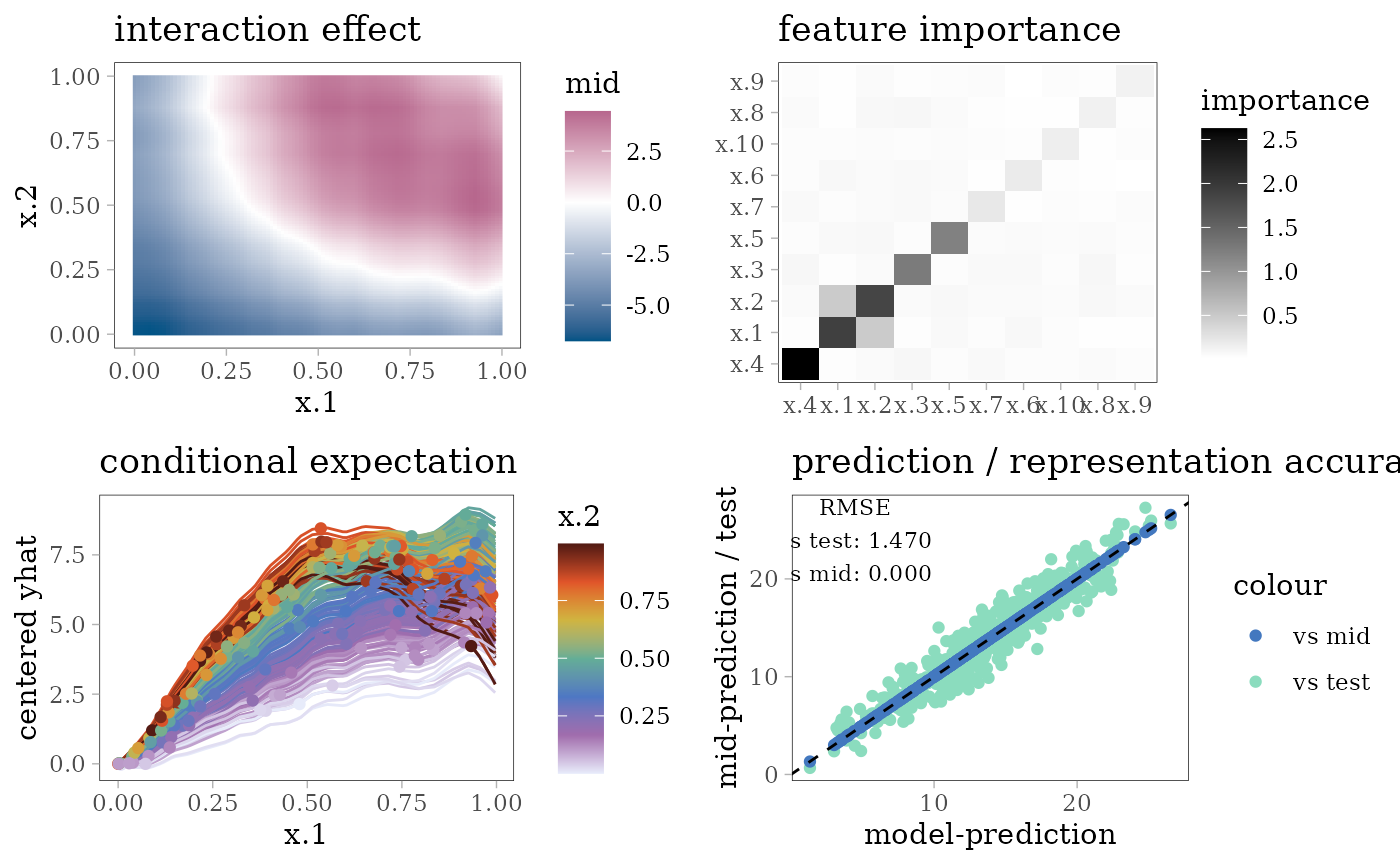

Compare Multiple Models 

p1 <- ggmid(ml[1:4], "x.1") + theme(legend.position = "none")
p2 <- ggmid(ml[1:4], "x.3") + theme(legend.position = "none")
p3 <- ggmid(ml[1:4], "x.4")
p4 <- ggmid(ml[5:8], "x.1") + theme(legend.position = "none")
p5 <- ggmid(ml[5:8], "x.3") + theme(legend.position = "none")
p6 <- ggmid(ml[5:8], "x.4")
(p1+ p2 + p3) / (p4 + p5 + p6)

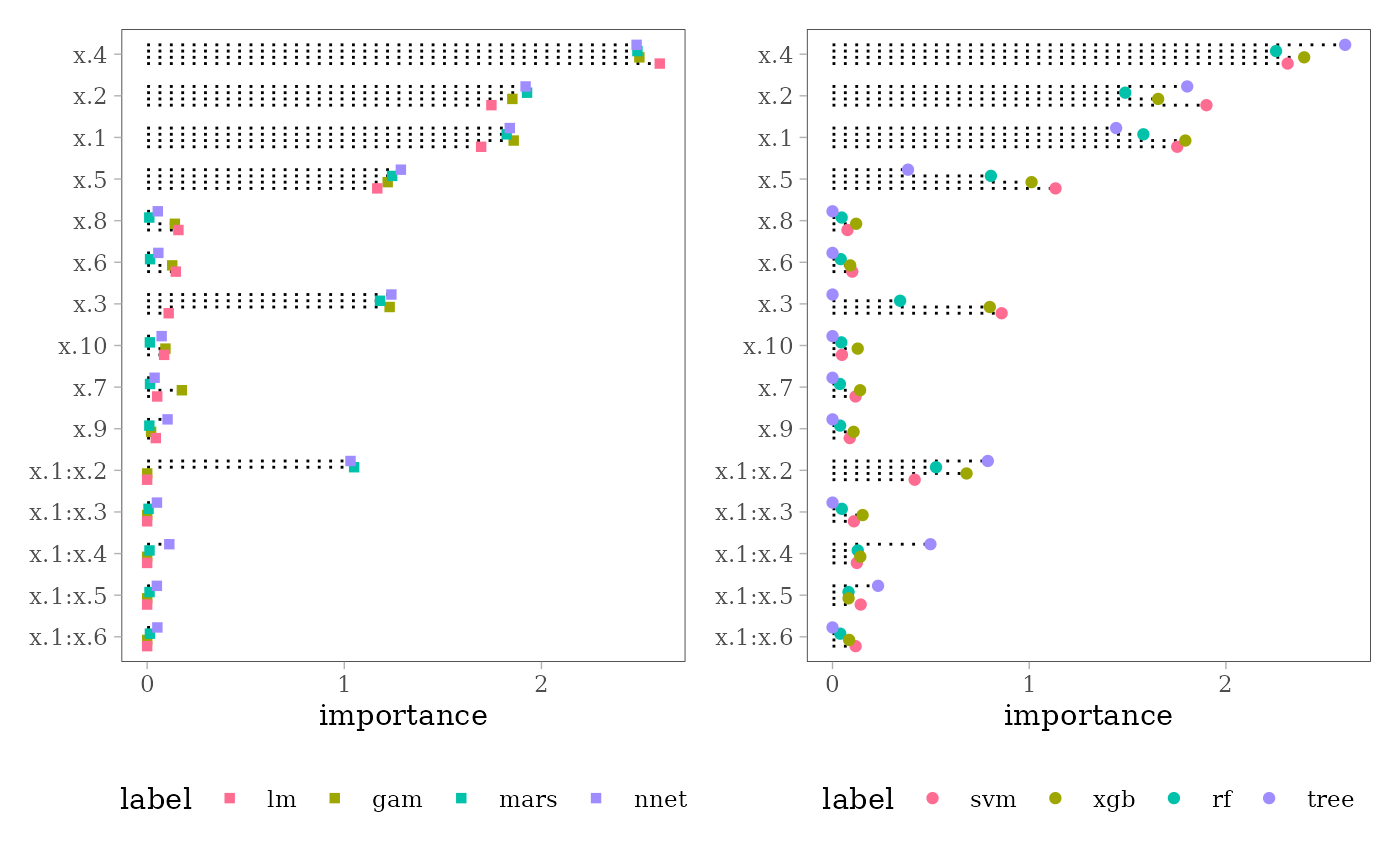
impl <- mid.importance(ml)
p1 <- ggmid(impl[1:4], type = "dotchart", pch = 15) +
  theme(legend.position = "bottom")
p2 <- ggmid(impl[5:8], type = "dotchart", terms = mid.terms(impl)) +
  theme(legend.position = "bottom")
p1 + p2