パッケージの概要
actuar パッケージは、(主に損害保険分野の)保険数理に関する機能を実装したパッケージです。actuar パッケージの特徴の一つは様々な確率分布を扱うための関数を実装していることで、パレート分布、Burr分布、対数ガンマ分布、対数ロジスティック分布など、裾の厚い分布が数多く収録されています。
stats パッケージと同様、actuar パッケージにおいても、それぞれの分布に対して、その名称に接頭辞 “d”、“p”、“r”、“q” を付けた関数が用意されています。接頭辞ごとに関数の機能が異なり、d****(x, ...) が密度関数、p****(x, ...) が累積分布関数、r****(n, ...) が乱数を生成する関数、q(p, ...) が分位点を返す関数です。
確率密度関数をプロットする
パレート分布(Pareto Distribution)
\texttt{dpareto}(x,{\alpha},{\theta})={{\alpha}{\theta}^{\alpha}}/{(x+\theta)^{\alpha+1}}
パレート分布 pareto は「全体の数値の大部分は、全体を構成するうちの一部の要素が生み出している」というパレートの法則を表現する確率分布で、裾の重い分布の代表例として知られています。アクチュアリーサイエンスの分野では、損害保険における高額な保険金支払いのモデリングで頻繁に用いられます。ほとんどの請求は少額である一方、ごく一部の請求が非常に高額になるような事象をうまく表現できるため、巨大な損失額が発生するリスクの分析に役立ちます。
Warning: package 'actuar' was built under R version 4.5.1
xlim <- c(0, 3)
ylim <- c(0, 2)
main <- "Pareto Distribution"
curve(dpareto(x, 1, 1), type = "l", lty = 1, col = "darkgray",
xlim = xlim, ylim = ylim, ylab = "", main = main)
curve(dpareto(x, 2, 1), type = "l", lty = 2, col = "darkcyan", add = TRUE)
curve(dpareto(x, 1, 2), type = "l", lty = 3, col = "darkred", add = TRUE)
curve(dpareto(x, 2, 2), type = "l", lty = 4, col = "darkblue", add = TRUE)
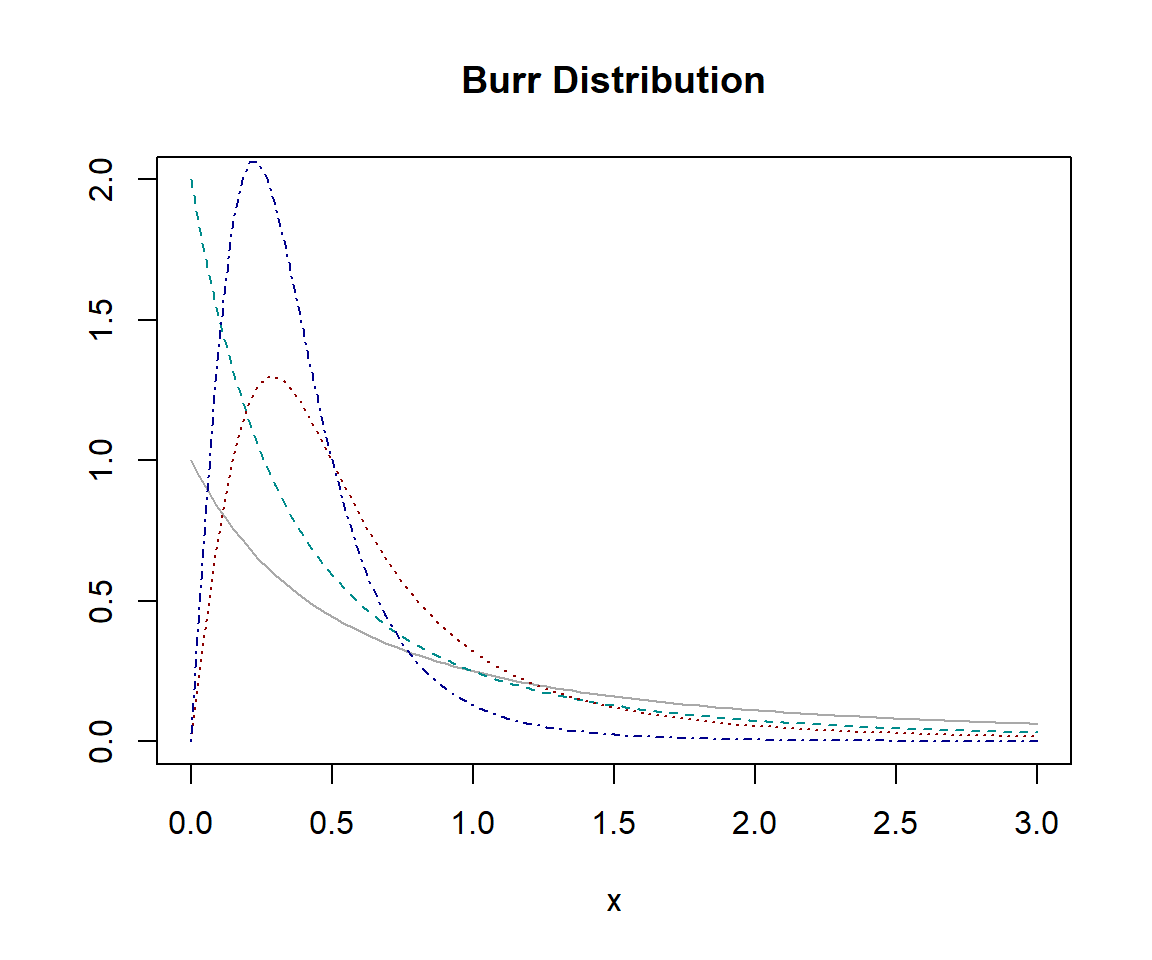
バー分布(Burr Distribution)
\texttt{dburr}(x,{\alpha},{\gamma},{\theta})={{\alpha}{\gamma}(x/{\theta})^{\gamma}}/{x[1+(x/{\theta)^{\gamma}}]^{\alpha + 1}}
バー分布 burr は非常に柔軟な確率分布で、多くの有名な分布(ガンマ分布、対数正規分布、パレート分布など)を特別な場合として含んだり、近似したりすることができます。裾の重さを調整できるため、パレート分布と同様に極端な損失のモデリングに役立ちますが、柔軟性のために、より多様なデータに対して適合が良い場合があります。そのため、損害額のモデリングにおいて強力な選択肢の一つとなります。
xlim <- c(0, 3)
ylim <- c(0, 2)
main <- "Burr Distribution"
curve(dburr(x, 1, 1, 1), type = "l", lty = 1, col = "darkgray",
xlim = xlim, ylim = ylim, ylab = "", main = main)
curve(dburr(x, 2, 1, 1), type = "l", lty = 2, col = "darkcyan", add = TRUE)
curve(dburr(x, 1, 2, 2), type = "l", lty = 3, col = "darkred", add = TRUE)
curve(dburr(x, 2, 2, 2), type = "l", lty = 4, col = "darkblue", add = TRUE)
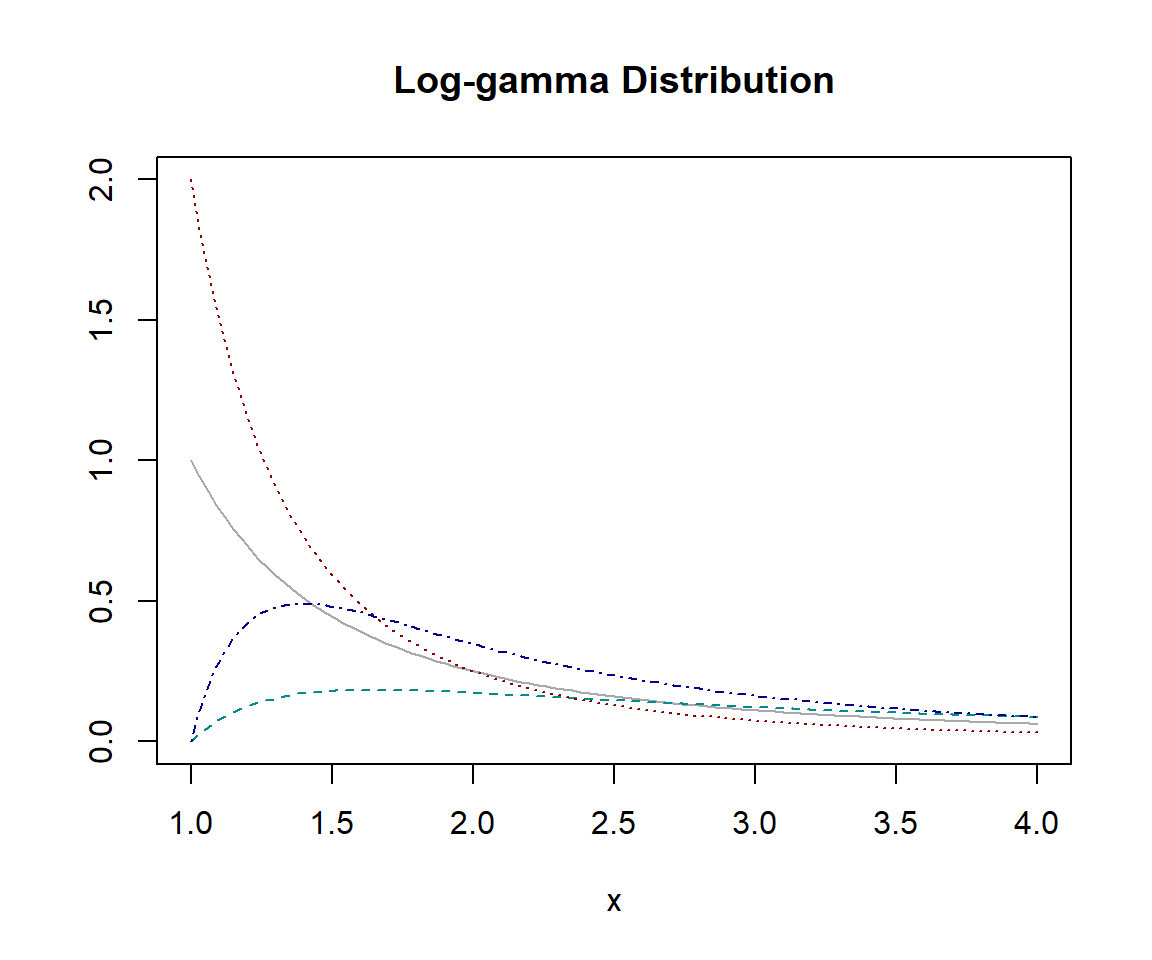
対数ガンマ分布(Log-gamma Distribution)
\texttt{dlgamma}(x,{\alpha},{\lambda})={{\lambda}^{\alpha}{\Gamma}({\alpha})}/{[(\log{x})^{\alpha-1}x^{\lambda+1}]}
actuar における対数ガンマ分布 lgamma は、対数をとるとガンマ分布に従う確率変数が従う分布、すなわち、\mathrm{X}がガンマ分布に従うときにe^{\mathrm{X}}が従う分布のことを指します。ガンマ分布が持つ柔軟な形状の特性を対数スケールで持つため、極端に大きな値が発生するような事象、たとえば巨額の保険金支払いや大規模な自然災害による損害額などのモデリングに利用できることがあります。
xlim <- c(1, 4)
ylim <- c(0, 2)
main <- "Log-gamma Distribution"
curve(dlgamma(x, 1, 1), type = "l", lty = 1, col = "darkgray",
xlim = xlim, ylim = ylim, ylab = "", main = main)
curve(dlgamma(x, 2, 1), type = "l", lty = 2, col = "darkcyan", add = TRUE)
curve(dlgamma(x, 1, 2), type = "l", lty = 3, col = "darkred", add = TRUE)
curve(dlgamma(x, 2, 2), type = "l", lty = 4, col = "darkblue", add = TRUE)
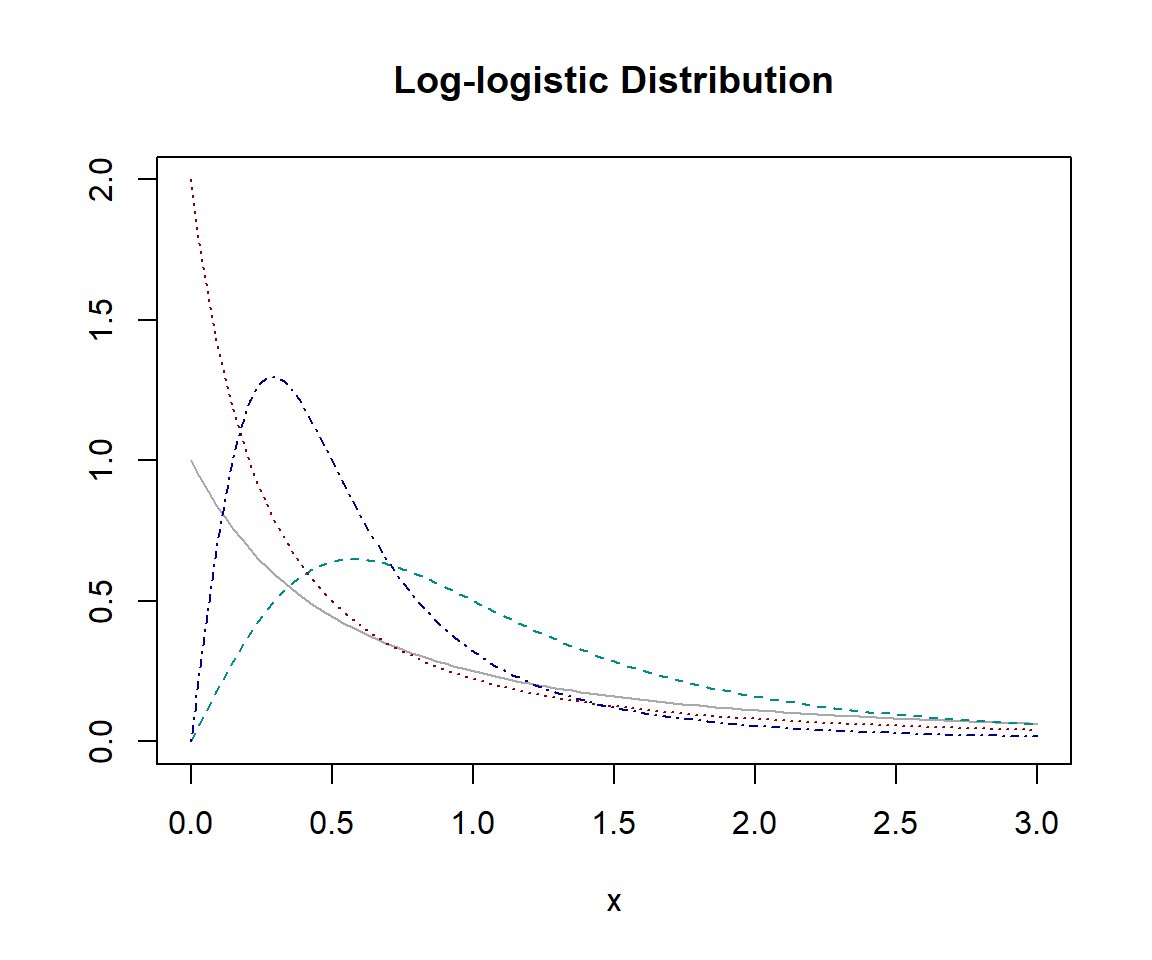
対数ロジスティック分布(Log-logistic Distribution)
\texttt{dllogis}(x,{\gamma},{\theta})={{\gamma}(x/{\theta})^{\gamma}}/{x[1+(x/{\theta)}]^2}
対数ロジスティック分布 llogis は、対数をとるとロジスティック分布(累積分布関数がロジスティック関数である連続分布)に従う確率変数の分布です。経済学の分野ではフィスク分布(Fisk Distribution)とも呼ばれます。この分布は対数正規分布と似たような山形の形状を取りますが、それよりも裾が重いという特徴を持ちます。この性質から、損害保険における損失額のモデリング、特に甚大な損害が発生する可能性を無視できない場合に優れた選択肢となりえます。
xlim <- c(0, 3)
ylim <- c(0, 2)
main <- "Log-logistic Distribution"
curve(dllogis(x, 1, 1), type = "l", lty = 1, col = "darkgray",
xlim = xlim, ylim = ylim, ylab = "", main = main)
curve(dllogis(x, 2, 1), type = "l", lty = 2, col = "darkcyan", add = TRUE)
curve(dllogis(x, 1, 2), type = "l", lty = 3, col = "darkred", add = TRUE)
curve(dllogis(x, 2, 2), type = "l", lty = 4, col = "darkblue", add = TRUE)
その他の分布
actuar パッケージには、上記のほかにも以下のような確率分布が実装されています。
| 逆ガンマ分布 |
invgamma |
| 逆パレート分布 |
invpareto |
| 逆バー分布 |
invburr |
| 逆ワイブル分布 |
invweibull |
| 逆指数分布 |
invexp |
| 一般化ベータ分布 |
genbeta |
| 一般化パレート分布 |
genpareto |