distrEx

確率分布/確率変数

Published

March 31, 2026

パッケージの概要

distrExは、確率変数をS4クラスで扱うことのできるパッケージdistrの機能を拡張するパッケージです。 distrで生成した確率変数に対して期待値・分散を計算する関数、多変量確率分布のクラス、確率変数間の距離を計算する関数などを提供します。

distrパッケージの使用方法

distrExはdistrの拡張機能であるため、distrの使用が前提となっています。本稿ではdistrExの機能に絞って解説を行いますので、distrの基本的な知識や使用方法はdistrのコード使用例をご参照ください。

パッケージの使用例

distrExの主な機能の使用例を紹介します。一部の数値例にirisデータセットを用います。

library(distr)

Loading required package: startupmsg

*** Utilities for Start-Up Messages ***

Version information in start-up messages is currently suppressed. To see such information on startup as in versions of this pkg prior to this versionr, set option "StartupBanner" to a value different to {"off", "no-version", "no - version"}, e.g., by options("StartupBanner" = "complete") or by options("StartupBanner" = NULL) or by options("StartupBanner" = "something else").
Detailed information about which packages are currently loaded or attached at which version (regardless of whether these have start-up messages managed by this package) can be obtained by "sessionInfo()".

Loading required package: sfsmisc

Warning: package 'sfsmisc' was built under R version 4.5.3

*** Object Oriented Implementation of Distributions ***


Attaching package: 'distr'

The following objects are masked from 'package:stats':

    df, qqplot, sd

library(distrEx)

*** Extensions of Package 'distr' ***


Attaching package: 'distrEx'

The following objects are masked from 'package:stats':

    IQR, mad, median, var

data(iris)
species_num <- as.numeric(iris$Species)
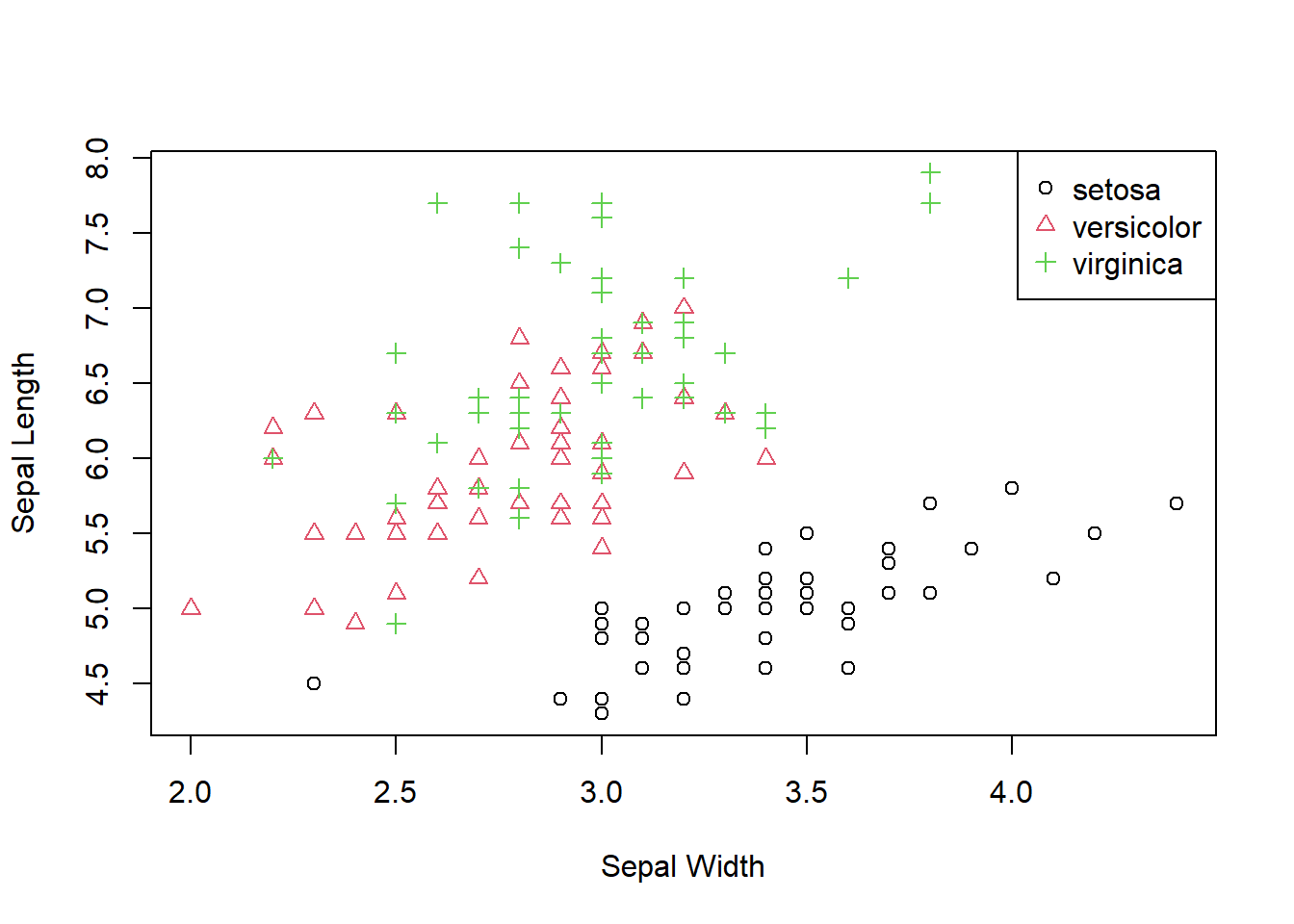
plot(x=iris$Sepal.Width, y=iris$Sepal.Length, 
     pch = species_num, col = species_num,
     xlab = "Sepal Width", ylab = "Sepal Length")
legend("topright", levels(iris$Species), pch = 1:3, col = 1:3)

期待値と分散

distrで生成した確率変数を引数にとり、当該確率変数の期待値を計算するE関数、および分散を計算するvar関数が用意されています。以下にいくつかの例を示します。

正規分布

X <- Norm(mean = 3, sd = 2)
cat(sprintf("期待値:%.2f 分散:%.2f", E(X), var(X)))

期待値:3.00 分散:4.00

ポアソン分布

N <- Pois(lambda = 4)
cat(sprintf("期待値:%.2f 分散:%.2f", E(N), var(N)))

期待値:4.00 分散:4.00

正規変数を変換した確率変数

X_affine <- X * 2 + 5
cat(sprintf("期待値:%.2f 分散:%.2f", E(X_affine), var(X_affine)))

期待値:11.00 分散:16.00

経験分布

d_setosa <- iris[iris$Species=="setosa",]
n <- nrow(d_setosa)

X_emp <- EmpiricalDistribution(data = d_setosa$Sepal.Length)
cat(sprintf("期待値:%.5f 分散:%.5f", E(X_emp), var(X_emp)))

期待値:5.00600 分散:0.12176

cat(sprintf("(経験分布との比較用)実データ  平均:%.5f 分散:%.5f", 
            mean(d_setosa$Sepal.Length), (n-1)/n*stats::var(d_setosa$Sepal.Length)))

(経験分布との比較用)実データ  平均:5.00600 分散:0.12176

E関数およびvar関数の誤差

distrExのE関数とvar関数は、AbsContDistributionなどの一般の分布のクラスに対しては、内部的には数値積分で処理されています。計算する確率変数の分布によっては数値的な誤差が無視できない大きさになる場合があるため、別の方法による計算結果との比較など、検証を行いながら使用することをおすすめします。

# 例. 指数分布に従うXの二乗の期待値
#X <- Norm(mean = 0, sd = 1)
X <- Exp(rate = 1)
X2 <- X^2

## 計算方法(1) distrExのE関数を直接適用
res_1 <- E(X2)

## 計算方法(2) 分散 + 期待値の二乗で計算
res_2 <- var(X) + E(X)^2

cat(sprintf("(1):%.5f (2):%.5f", res_1, res_2))

(1):1.79658 (2):2.00000

多変量分布

distrExには多変量分布を表現するためのクラスが用意されています。これらの分布についても、例えばE関数を適用して、変数ごとの期待値を計算することも可能です。以下ではdistrExに用意されている多変量分布の例として、経験多変量分布と条件付分布のクラスを紹介します。

経験多変量分布

多変量のデータを引数として与えることで、経験多変量分布を生成できます。以下の例では、経験多変量分布を生成し、生成した多変量分布に対してE関数で期待値を算出しています。

X <- EmpiricalMVDistribution(
  data = as.matrix(iris[iris$Species == "setosa", c("Sepal.Length", "Sepal.Width")]))

Warning in DiscreteMVDistribution(supp = data, Symmetry = Symmetry): collapsing
to unique support values

E(X)

Sepal.Length  Sepal.Width 
       5.006        3.428

条件付分布

distrExに用意されている条件付分布の一つが線形モデルです。次の例では、比較用にR標準の線形モデルを構築したうえで、distrExのLMCondDistributionクラスを使用して、 Sepal.LengthをSepal.Widthで回帰した線形モデルに従う確率変数Xを生成しています。

# R標準の線形モデル
d_setosa <- iris[iris$Species == "setosa",]
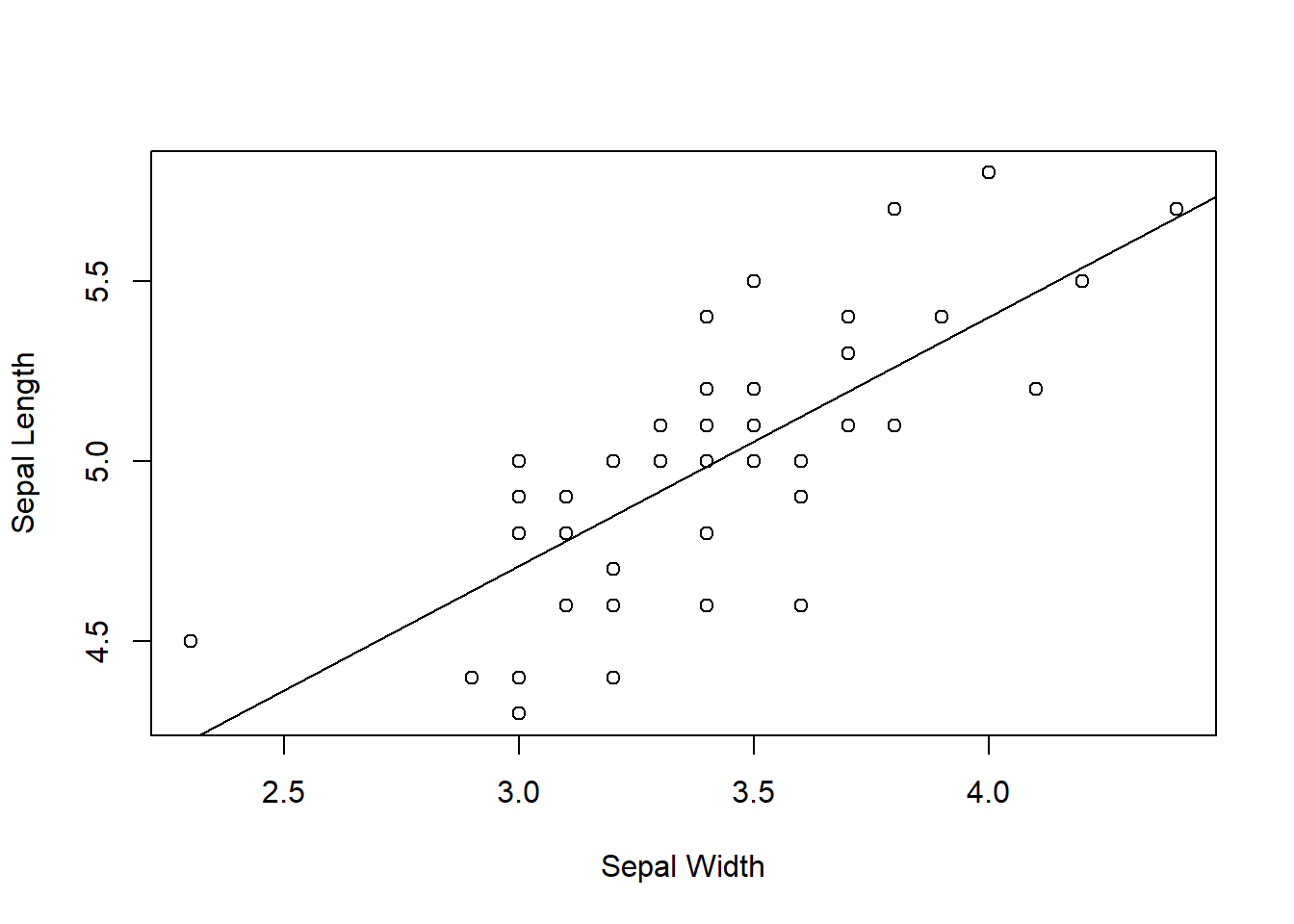
lm.model <- lm(Sepal.Length ~ Sepal.Width, data = d_setosa)
plot(d_setosa$Sepal.Width, d_setosa$Sepal.Length, xlab="Sepal Width", ylab="Sepal Length")
abline(lm.model)

# distrExの確率変数として生成
X <- LMCondDistribution(Error = Norm(sd = var(lm.model$residuals)), 
                   theta = lm.model$coefficients[2],
                   intercept = lm.model$coefficients[1])

条件付分布に対しては、E関数の条件付期待値の機能が使用できます。すなわちこの例の場合、線形モデルにおいて特定のSepal.Widthの値の下での、Sepal.lengthの期待値を計算します。 distrExのE関数で計算した条件付期待値は、R標準のpredict関数を線形モデルに適用した予測値とほぼ一致していることが確認できます。

# distrExのE関数による条件付期待値と、R標準による線形モデルのpredict
cat(sprintf("distrEx : %.5f\nR標準 : %.5f",
            E(X, cond = 3.5), predict(lm.model, list(Sepal.Width = 3.5))))

distrEx : 5.05571
R標準 : 5.05572

確率分布間の距離

distrExには確率変数が従う確率分布間の距離を計算する関数が用意されています。以下はKolmogorovDist関数を使用した、Kolmogorov距離の計算例です。
(二つの分布関数FとGに対して、d(F,G) = sup|F(x)-G(x)|)
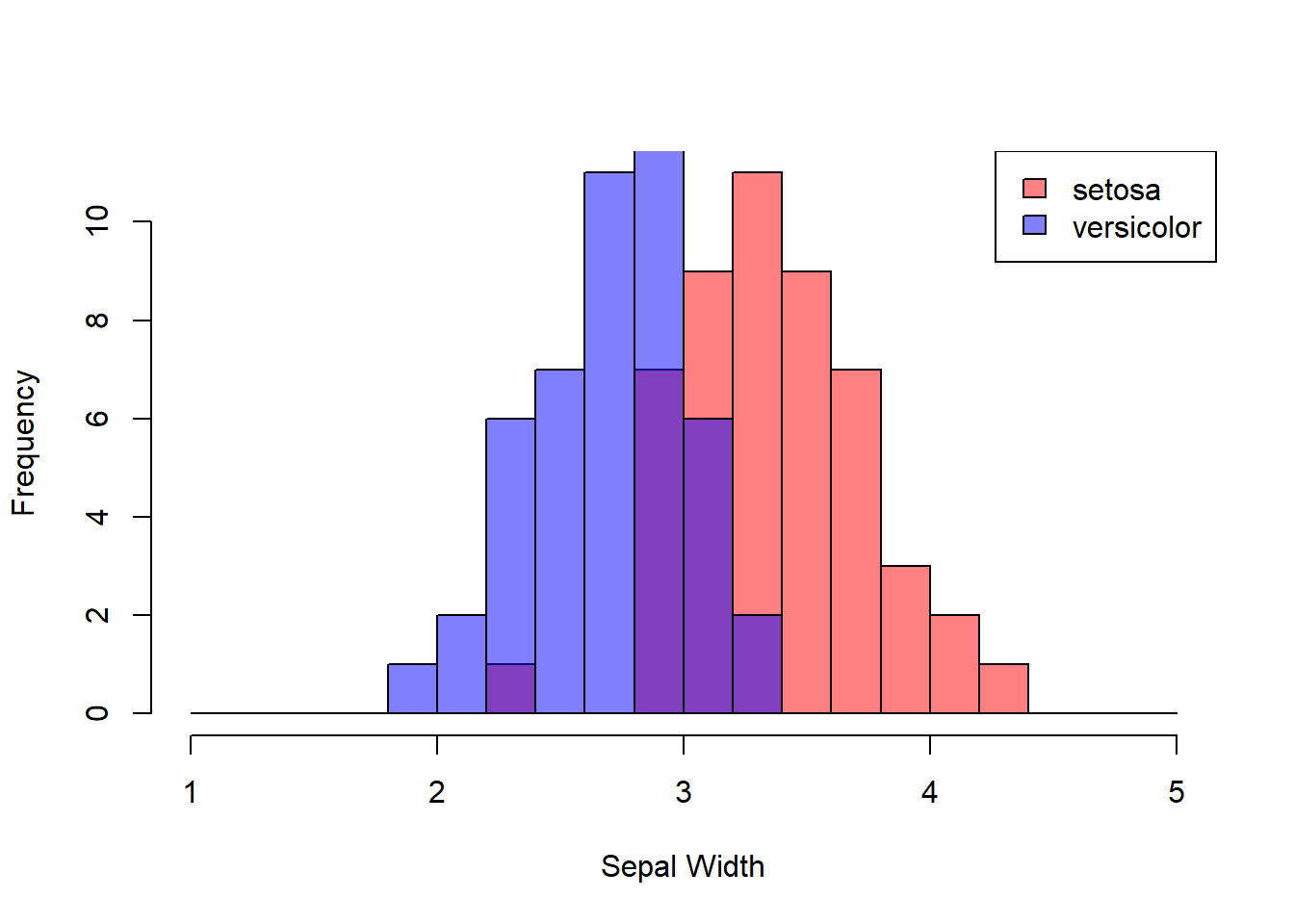
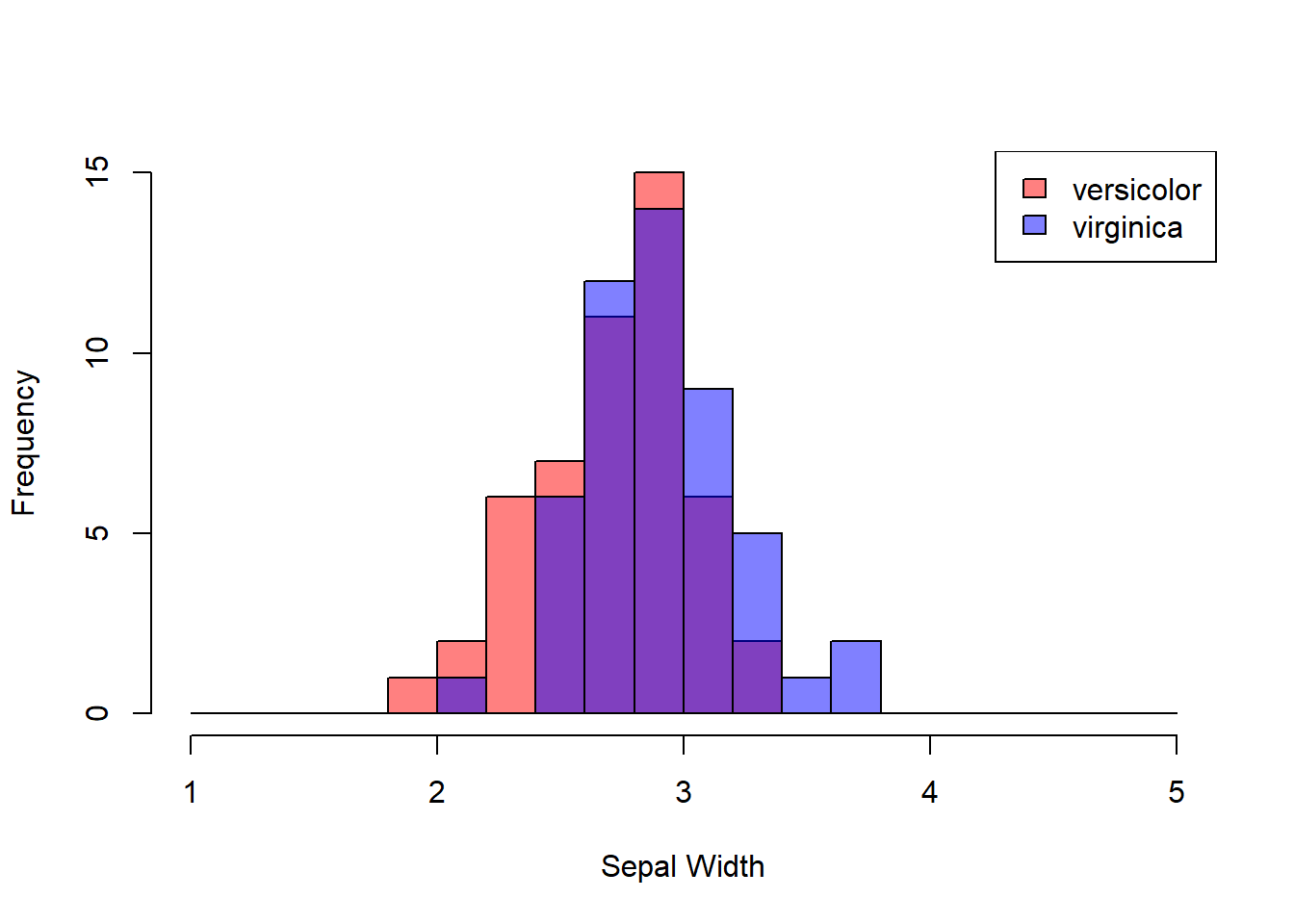
irisのSepal.Widthについて、Speceies間の経験分布の距離を計算しています。グラフ上でも度数分布の重なりが大きいversicolorとvirginica間の経験分布の距離が、setosaとversicolor間の距離より小さい結果となっています。

X_setosa <- EmpiricalDistribution(
  data = as.matrix(iris[iris$Species == "setosa", "Sepal.Width"]))
X_versicolor <- EmpiricalDistribution(
  data = as.matrix(iris[iris$Species == "versicolor", "Sepal.Width"]))
X_virginica <- EmpiricalDistribution(
  data = as.matrix(iris[iris$Species == "virginica", "Sepal.Width"]))

cols <- c("#FF00007F", "#0000FF7F")

# setosa vs versicolor
hist(iris[iris$Species == "setosa", "Sepal.Width"], 
     breaks=seq(1, 5, 0.2), col=cols[1], main="", xlab="Sepal Width")
hist(iris[iris$Species == "versicolor", "Sepal.Width"],
     breaks=seq(1, 5, 0.2), col=cols[2], add=TRUE, main="", xlab="")
legend("topright",legend=c("setosa", "versicolor"), fill=cols, )

# Kolmogorov距離
KolmogorovDist(X_setosa, X_versicolor)

Kolmogorov distance 
               0.68

# versicolor vs virginica
hist(iris[iris$Species == "versicolor", "Sepal.Width"], 
     breaks=seq(1, 5, 0.2), col=cols[1], main="", xlab="Sepal Width")
hist(iris[iris$Species == "virginica", "Sepal.Width"],
     breaks=seq(1, 5, 0.2), col=cols[2], add=TRUE, main="", xlab="")
legend("topright",legend=c("versicolor", "virginica"), fill=cols, )

# Kolmogorov距離
KolmogorovDist(X_versicolor, X_virginica)

Kolmogorov distance 
               0.26

なお、紹介したKolmogorov距離以外にも様々な距離関数が用意されているため、詳細はマニュアル[1]をご参照ください。

参考資料

[1] Peter Ruckdeschel, Matthias Kohl, Thomas Stabla & Florian Camphausen. S4 Classes for Distributions—a manual for packages.