ismevは、極値理論に基づく統計解析を行うためのパッケージです。 Stuart Colesによる極値理論を紹介する著書『An Introduction to Statistical Modeling of Extreme Values』に登場する計算をサポートする関数が含まれています。 極値理論は、分布から大きく外れるような極端な事象をモデル化するための手法であり、保険分野においても、再保険や巨大自然災害リスクの分析、リスク管理でのテイル評価等に利用されています。
ブロック最大値モデルは、同一分布からの独立な標本の最大値の確率的性質を扱うモデルです。 ここでは、ismevパッケージに入っているportpirieのデータセットを使って、一般化極値分布（GEV）のフィッティングを行います。 portpirieは、65行2列で構成されるデータセットであり、1923年から1987年までの南オーストラリアのポートピリーで記録された年間最大海面水位を示しています。1列目は対応する年を示しています。年ごとの最大値のデータとなっているため、このままGEVのフィッティングを行います。フィッティングにはgev.fit関数を使います。
# データセット"portpirie"を取得
data(portpirie)
head(portpirie) Year SeaLevel
1 1923 4.03
2 1924 3.83
3 1925 3.65
4 1926 3.88
5 1927 4.01
6 1928 4.08# ヒストグラムを表示
hist(portpirie$SeaLevel)
# "portpirie"の年間最大海面水位についてGEVフィッティング
fit_portpirie <- gev.fit(portpirie$SeaLevel)$conv
[1] 0
$nllh
[1] -4.339058
$mle
[1] 3.87474692 0.19804120 -0.05008773
$se
[1] 0.02793211 0.02024610 0.09825633gev.fit関数によるフィッティング結果の見方は次のとおりです。
$conv
$nllh
$mle
$se
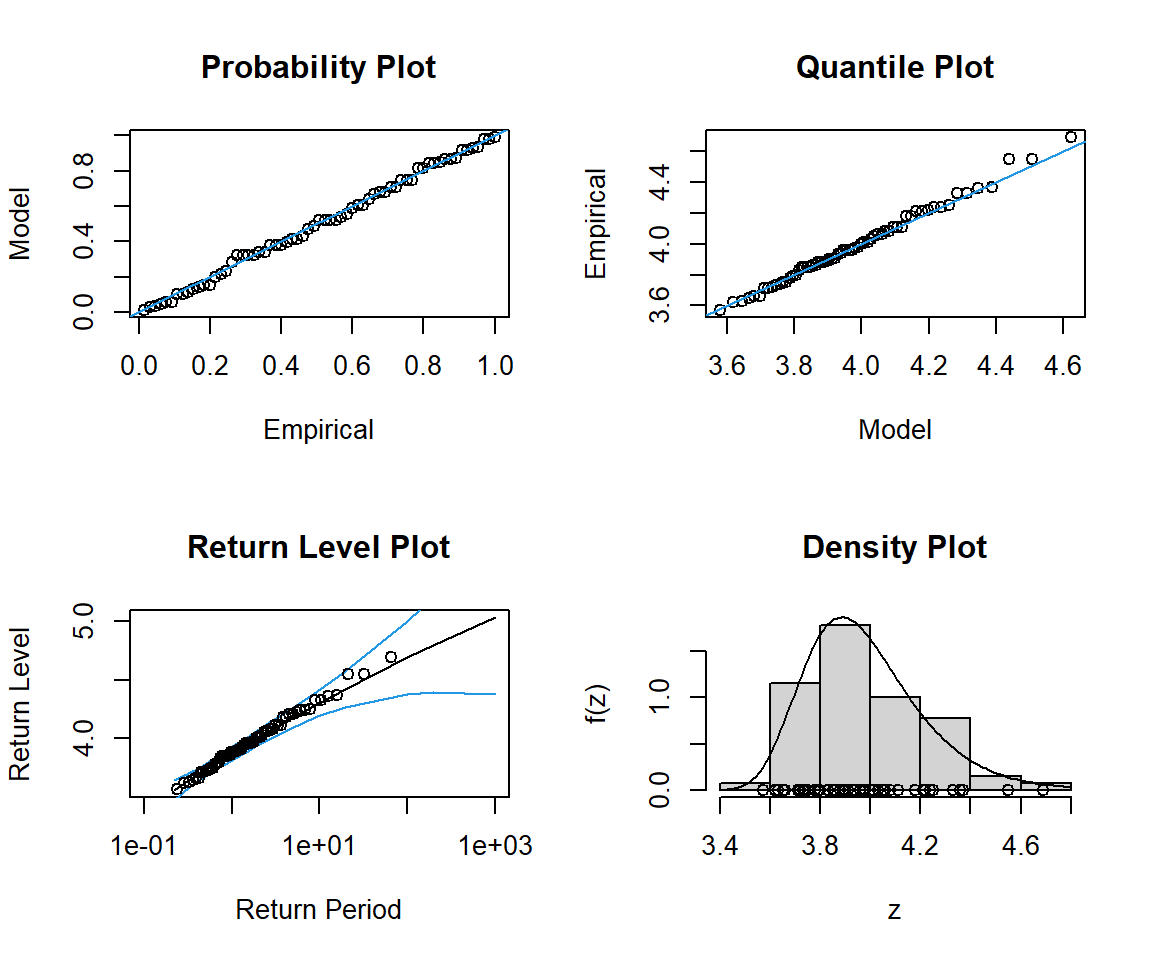
次に、gev.diag関数を用いて、先ほど作成したGEVモデルについて、データに適合しているかどうかを視覚的および統計的に評価します。 gev.diag関数により、P-Pプロット、Q-Qプロット、再現レベルプロット、データのヒストグラムと適合した密度を出力することができます。
gev.diag(fit_portpirie)
次に、指数分布に従う乱数から作成した最大値のデータに対して、GEVフィッティングを行います。理論的には、最大値M_nを正規化した値Z_nはグンベル分布に法則収束するはずです。
# シード値を設定
set.seed(1234)
# λ = 2 の指数分布に従う乱数を100万個生成
N <- 1000000
lambda <- 2
random_exp <- rexp(N, rate = lambda)
# ヒストグラムを表示
hist(random_exp)
# 1000個ずつのブロックに分けて、各ブロックの最大値を計算
n <- 1000
max_exp <- tapply(random_exp, (seq_along(random_exp) - 1) %/% n + 1, max)
# 各ブロックの最大値M_nをデータフレームに格納
df_max_exp <- data.frame(Block = 1:length(max_exp), M_n = max_exp)
# M_nを正規化した値Z_nをデータフレームに格納
d_n <- log(n) / lambda
c_n <- 1 / lambda
df_max_exp$Z_n <- (df_max_exp$M_n - d_n) / c_n
# データフレームの最初の数行を表示
head(df_max_exp) Block M_n Z_n
1 1 3.633542 0.3593291
2 2 3.730824 0.5538925
3 3 3.123590 -0.6605744
4 4 3.188098 -0.5315598
5 5 3.621496 0.3352366
6 6 3.186516 -0.5347237# 生成したデータフレームについてGEVフィッティング
fit_max_exp <- gev.fit(df_max_exp$Z_n)$conv
[1] 0
$nllh
[1] 1578.983
$mle
[1] -0.043063270 0.996804717 0.006797281
$se
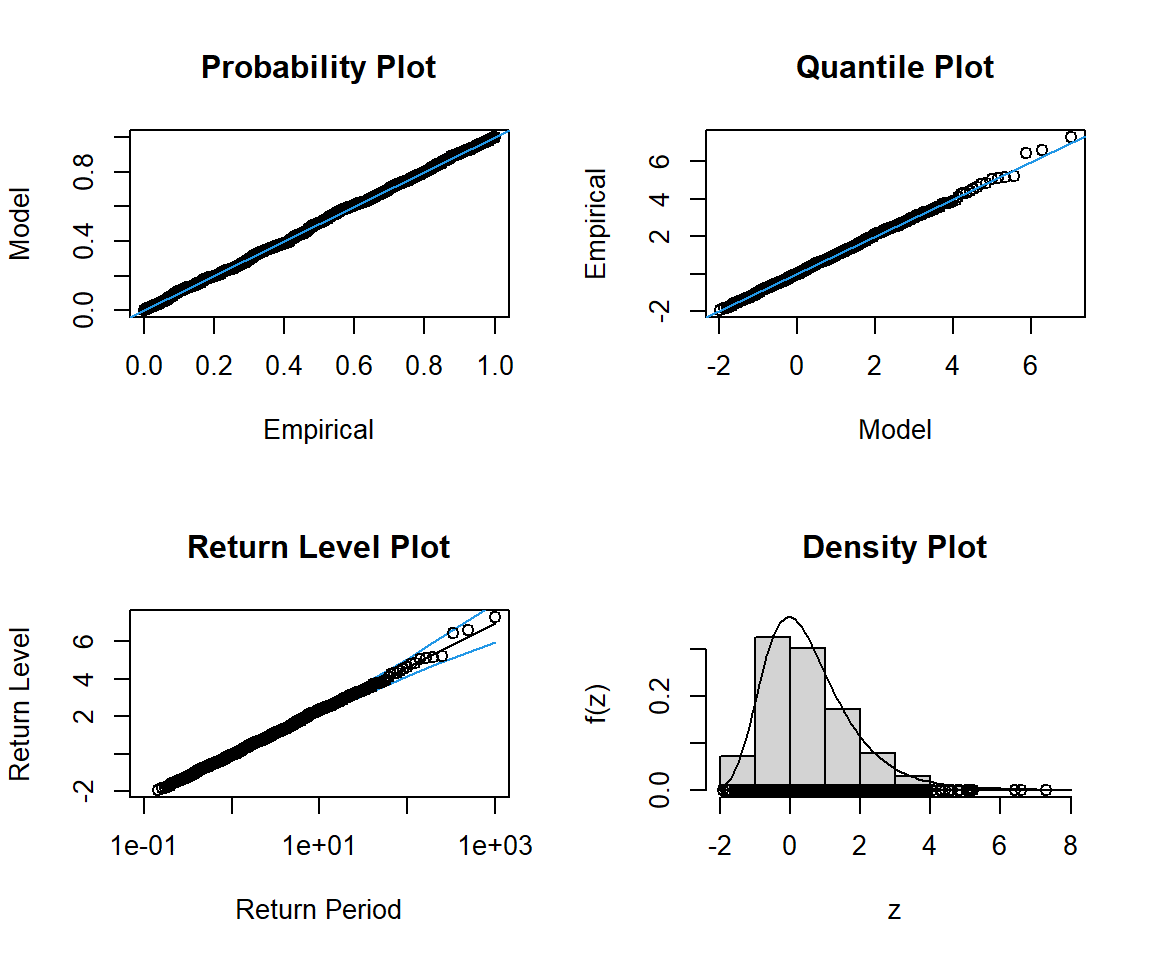
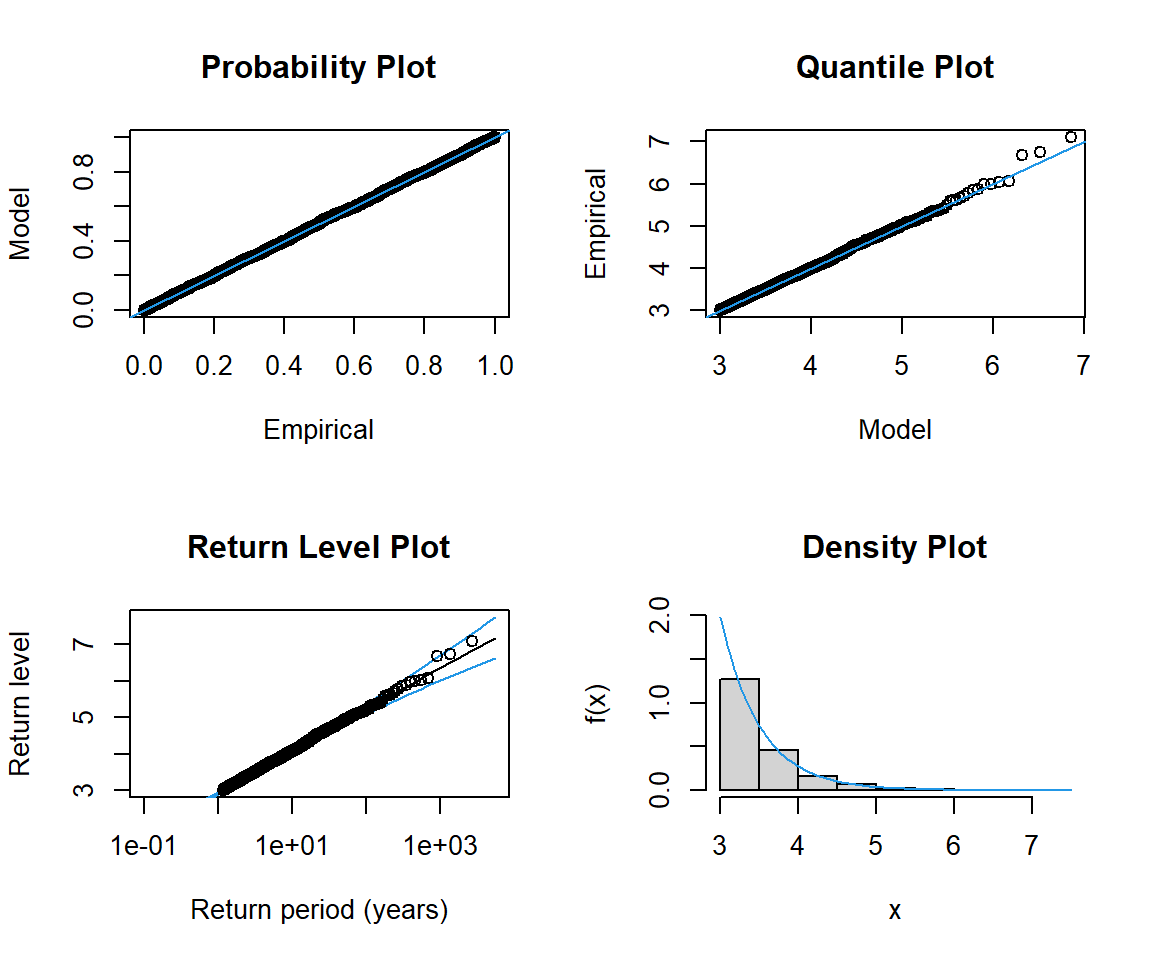
[1] 0.03540953 0.02575965 0.02287590# フィッティング結果を評価
gev.diag(fit_max_exp)
\mu \fallingdotseq 0、\sigma\fallingdotseq 1、\xi\fallingdotseq 0となり、グンベル分布が概ね再現できました。
閾値超過モデルはある閾値を超過したデータを対象とするモデルです。 先ほど生成した指数分布に従う乱数データを用いて、閾値超過モデルである一般化パレート分布（GPD）のフィッティングを行います。
# 乱数データをデータフレームに格納
df_random_exp <- data.frame(X = random_exp)
# 結果を確認
head(df_random_exp) X
1 1.250879302
2 0.123379442
3 0.003290978
4 0.871373045
5 0.193591292
6 0.044974836# 閾値を設定
u <- 3
# 生成したデータフレームについてGPDフィッティング
fit_excess_exp <- gpd.fit(df_random_exp$X, u)$threshold
[1] 3
$nexc
[1] 2378
$conv
[1] 0
$nllh
[1] 740.2906
$mle
[1] 0.504669635 -0.004868447
$rate
[1] 0.002378
$se
[1] 0.01463252 0.02049923gpd.fit関数によるフィッティング結果の見方は、gev.fit関数と共通する箇所もありますが、次のとおりです。形状パラメータ\xiが0に近い数値となっており、想定どおり指数分布の形状を示す結果となっています。
$threshold
$nexc
$conv
$nllh
$mle
$rate
$se
GPDにおいても、次のとおりgpd.diag関数により作成したモデルについて評価することが可能です。出力内容はgev.diagと同じです。
# フィッティング結果を評価
gpd.diag(fit_excess_exp)
gpd.fit関数では閾値を自分で設定する必要があります。適切な閾値を選択する方法はいくつか考えられますが、gpd.fitrange関数を使えば、異なる閾値に対してGPDを適合させ、パラメータの推定値の変化を調べることができます。2つのパラメータが安定するように閾値を設定することでより信頼性の高いフィッティングが可能になります。
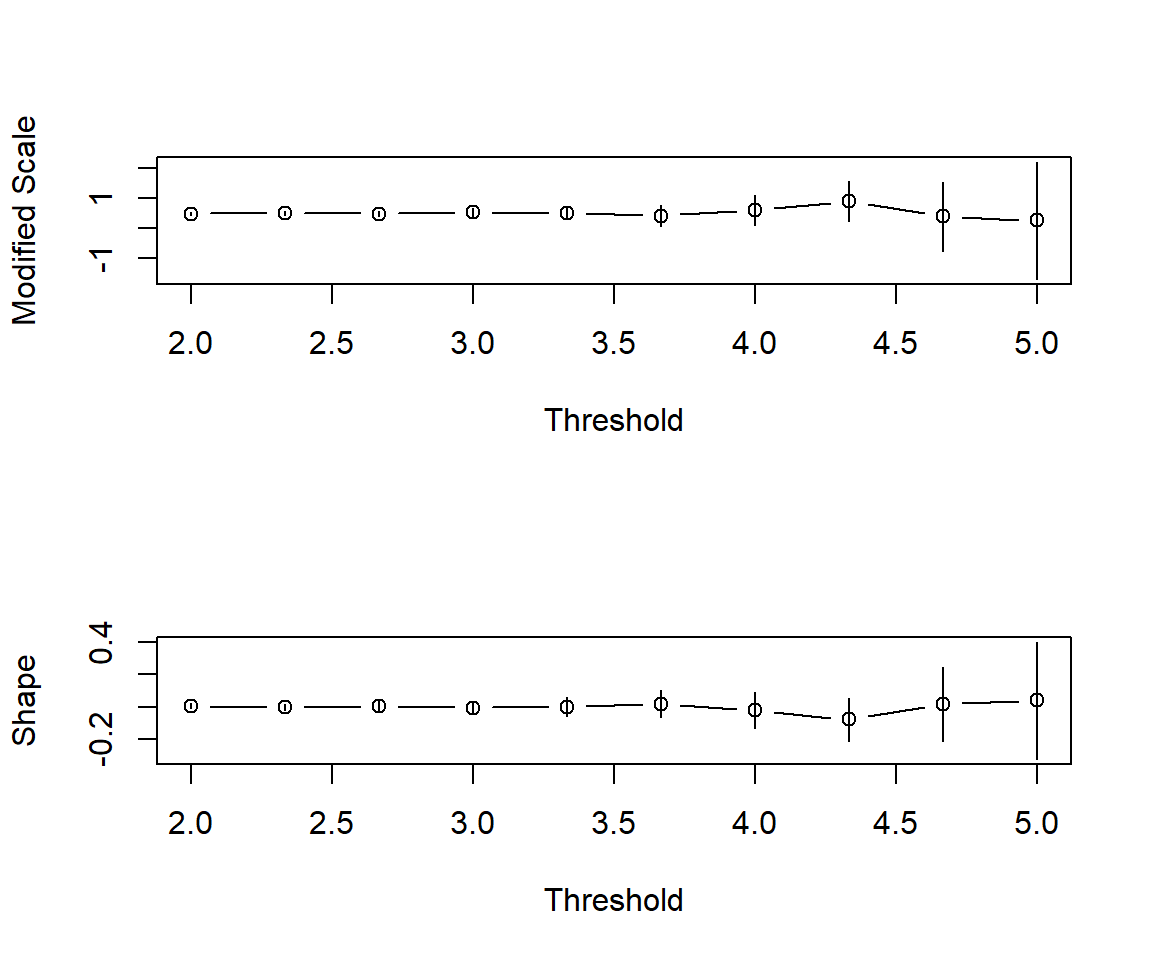
# 閾値が2～5の場合のパラメータ推定値を出力
gpd.fitrange(df_random_exp$X, 2, 5)
上記の結果では、閾値が4に差し掛かる辺りから信頼区間が急激に広がり不安定になることがわかります。このため、3～3.5の辺りで閾値を設定することが考えられます。
[1] Stuart Coles. An Introduction to Statistical Modeling of Extreme Values.
[2] 日本アクチュアリー会. 損保数理.