パッケージの概要
modeldataには、Rにおけるモデリングや機械学習のためのツール群として有名なtidymodelsパッケージ[1]のドキュメントやテストに使用されたデータセットが含まれており、これらは様々な機械学習や予測モデリングのサンプルデータとしても活用することができます。 また、データセットそのものに加え、分類や回帰課題のためのシミュレーションデータを生成する関数も含まれています。
パッケージの使用例
データセット
modeldataには様々なデータセットが用意されています。 データセットは以下のように、データセット名を指定してロードすることができます。
Attaching package: 'modeldata'
The following object is masked from 'package:datasets':
penguins
data("Chicago", package = "modeldata")
str(Chicago)
Classes 'tbl_df', 'tbl' and 'data.frame': 5698 obs. of 50 variables:
$ ridership : num 15.7 15.8 15.9 15.9 15.4 ...
$ Austin : num 1.46 1.5 1.52 1.49 1.5 ...
$ Quincy_Wells : num 8.37 8.35 8.36 7.85 7.62 ...
$ Belmont : num 4.6 4.72 4.68 4.77 4.72 ...
$ Archer_35th : num 2.01 2.09 2.11 2.17 2.06 ...
$ Oak_Park : num 1.42 1.43 1.49 1.45 1.42 ...
$ Western : num 3.32 3.34 3.36 3.36 3.27 ...
$ Clark_Lake : num 15.6 15.7 15.6 15.7 15.6 ...
$ Clinton : num 2.4 2.4 2.37 2.42 2.42 ...
$ Merchandise_Mart: num 6.48 6.48 6.41 6.49 5.8 ...
$ Irving_Park : num 3.74 3.85 3.86 3.84 3.88 ...
$ Washington_Wells: num 7.56 7.58 7.62 7.36 7.09 ...
$ Harlem : num 2.65 2.76 2.79 2.81 2.73 ...
$ Monroe : num 5.67 6.01 5.79 5.96 5.77 ...
$ Polk : num 2.48 2.44 2.53 2.45 2.57 ...
$ Ashland : num 1.32 1.31 1.32 1.35 1.35 ...
$ Kedzie : num 3.01 3.02 2.98 3.01 3.08 ...
$ Addison : num 2.5 2.57 2.59 2.53 2.56 ...
$ Jefferson_Park : num 6.59 6.75 6.97 7.01 6.92 ...
$ Montrose : num 1.84 1.92 1.98 1.98 1.95 ...
$ California : num 0.756 0.781 0.812 0.776 0.789 0.37 0.274 0.473 0.844 0.835 ...
$ temp_min : num 15.1 25 19 15.1 21 19 15.1 26.6 34 33.1 ...
$ temp : num 19.4 30.4 25 22.4 27 ...
$ temp_max : num 30 36 28.9 27 32 30 28.9 41 43 36 ...
$ temp_change : num 14.9 11 9.9 11.9 11 11 13.8 14.4 9 2.9 ...
$ dew : num 13.4 25 18 10.9 21.9 ...
$ humidity : num 78 79 81 66.5 84 71 74 93 93 89 ...
$ pressure : num 30.4 30.2 30.2 30.4 29.9 ...
$ pressure_change : num 0.12 0.18 0.23 0.16 0.65 ...
$ wind : num 5.2 8.1 10.4 9.8 12.7 12.7 8.1 8.1 9.2 11.5 ...
$ wind_max : num 10.4 11.5 19.6 16.1 19.6 17.3 13.8 17.3 23 16.1 ...
$ gust : num 0 0 0 0 0 0 0 0 0 0 ...
$ gust_max : num 0 0 0 0 25.3 26.5 0 26.5 31.1 0 ...
$ percip : num 0 0 0 0 0 0 0 0 0 0 ...
$ percip_max : num 0 0 0 0 0 0 0 0.07 0.11 0.01 ...
$ weather_rain : num 0 0 0 0 0 ...
$ weather_snow : num 0 0 0.214 0 0.516 ...
$ weather_cloud : num 0.708 1 0.357 0.292 0.452 ...
$ weather_storm : num 0 0.2083 0.0714 0.0417 0.4516 ...
$ Blackhawks_Away : num 0 0 0 0 0 0 0 0 0 0 ...
$ Blackhawks_Home : num 0 0 0 0 0 0 0 0 0 0 ...
$ Bulls_Away : num 0 0 1 0 0 0 0 0 1 0 ...
$ Bulls_Home : num 0 1 0 0 0 1 0 0 0 0 ...
$ Bears_Away : num 0 0 0 0 0 0 0 0 0 0 ...
$ Bears_Home : num 0 0 0 0 0 0 0 0 0 0 ...
$ WhiteSox_Away : num 0 0 0 0 0 0 0 0 0 0 ...
$ WhiteSox_Home : num 0 0 0 0 0 0 0 0 0 0 ...
$ Cubs_Away : num 0 0 0 0 0 0 0 0 0 0 ...
$ Cubs_Home : num 0 0 0 0 0 0 0 0 0 0 ...
$ date : Date, format: "2001-01-22" "2001-01-23" ...
以下は格納されているデータセットの一覧です。(バージョン1.4.0時点です。) 各データのカラムやデータソース等の詳細は、modeldataのリファレンス[2]をご参照ください。
| Chicago stations |
シカゴの鉄道乗客数データ |
5698
20
|
50
1
|
| Sacramento |
サクラメント市(カリフォルニア州)の住宅価格 |
932
|
9
|
| Smithsonian |
スミソニアン博物館のジオコードデータ |
20
|
3
|
| ad_data |
アルツハイマー病に関する333患者のデータ |
333
|
131
|
| ames |
エイムズ市(アイオワ州)の住宅データ |
2930
|
74
|
| attrition |
従業員の離職に関するデータ |
1470
|
31
|
| biomass |
バイオマス燃料のデータ |
536
|
8
|
| bivariate_test bivariate_train bivariate_val |
二値分類用データの例 |
710
1009
300
|
3
3
3
|
| car_prices |
ケリー・ブルー・ブック社によるGM車のリセールデータ |
804
|
18
|
| cat_adoption |
保護猫の譲渡に関するデータ |
2257
|
20
|
| cells |
細胞体の分類 |
2019
|
58
|
| check_times |
rパッケージの実行時間のデータ |
13626
|
25
|
| chem_proc_yield |
化学製品の整合工程に関するデータセット |
176
|
58
|
| concrete |
コンクリート混合物の圧縮強度 |
1030
|
9
|
| covers |
森林の主要な樹木に関する未加工のテキストデータ |
40
|
1
|
| credit_data |
信用リスクの分類用データ |
4454
|
14
|
| crickets |
コオロギが鳴く頻度と気温の関係 |
31
|
3
|
| deliveries |
フード・デリバリーの配送時間のデータ |
10012
|
31
|
| drinks |
アルコール類の売上の時系列データ |
309
|
2
|
| grants_2008 grants_other grants_test |
学術助成金の採択/非採択のデータ |
6633
8190
518
|
1
1503
1503
|
| hepatic_injury_qsar |
肝臓損傷の分類用データ |
281
|
377
|
| hotel_rates |
リスボンにおけるホテル料金のデータ |
15402
|
28
|
| hpc_cv |
高性能計算(HPC)環境における実行時間のクラス確率の予測 |
3467
|
7
|
| hpc_data |
高性能計算(HPC)環境における実行時間のクラス分類用データ |
4331
|
8
|
| ischemic_stroke |
虚血性脳卒中の有無を予測するためのデータ |
126
|
29
|
| leaf_id_flavia |
葉のイメージデータの特徴量から植物の種を特定するデータ |
1907
|
59
|
| lending_club |
レンディング・クラブ・サービスのローンデータ |
9857
|
23
|
| meats |
肉サンプルの脂肪含有量、水分含有量、タンパク質含有量 |
215
|
103
|
| mlc_churn |
顧客の解約に関するデータ |
5000
|
20
|
| oils |
市販の油の脂肪酸濃度 |
96
|
8
|
| parabolic |
放物線状の境界を持つ二値分類データ |
500
|
3
|
| pathology |
肝臓の病理データ |
344
|
2
|
| pd_speech |
パーキンソン病患者の発話の分類データ |
252
|
752
|
| penguins |
パーマー基地のペンギンのデータ |
344
|
7
|
| permeability_qsar |
分子構造に関する化学情報から透過性を予測するデータ |
165
|
1108
|
| scat |
動物の糞の形態計測データ |
110
|
19
|
| solubility_test |
多変量適応的回帰スプライン(MARS)モデルによる溶解度の予測 |
316
|
2
|
| stackoverflow |
Stack Overflowによる年次サーベイのデータ |
5594
|
21
|
| steroidogenic_toxicity |
ステロイド生成毒性を評価するためのin vitroアッセイデータ |
162
|
13
|
| tate_text |
テート・ギャラリーの近現代美術作品のメタデータ |
4284
|
5
|
| taxi |
シカゴのタクシーのデータセット |
10000
|
7
|
| testing_data training_data |
Amazonの食品レビューのデータ |
1000
4000
|
3
3
|
| two_class_dat |
2クラス分類用に人工的に作成したデータ |
791
|
3
|
| two_class_example |
2クラス分類の予測値 |
500
|
4
|
| wa_churn |
IBMワトソンのサイトから取得した顧客解約データ |
7043
|
20
|
データ生成関数
modeldataには前項で紹介したデータセットに加え、データを生成するための関数も用意されています。
sim_classification
sim_classification関数は、二値分類用のシミュレーションデータを生成します。
以下はデータ生成の実行例です。 引数methodには生成方法を指定しますが、バージョン1.4.0時点では”caret”が唯一のオプションとなっており、caretパッケージ[3]のcaret::twoClassSim()関数と同じ生成方法が実装されています。
set.seed(1234)
d1 <- sim_classification(
num_samples = 100, # 生成するレコード数(デフォルトは100)
method = "caret", # 生成方法(デフォルトは"caret")
intercept = -5, # クラスの偏りをコントロールする(デフォルトは-5)
num_linear = 2, # クラス分類に無相関の変数linear_nの数(デフォルトは10)
keep_truth = TRUE # class_1のクラス確率の出力有無(デフォルトはFALSE)
)
str(d1)
tibble [100 × 9] (S3: tbl_df/tbl/data.frame)
$ class : Factor w/ 2 levels "class_1","class_2": 1 2 1 1 2 2 2 2 2 2 ...
$ two_factor_1: num [1:100] -1.796 0.637 1.354 -2.716 1.04 ...
$ two_factor_2: num [1:100] -1.3053 0.0755 1.432 -3.3104 0.0626 ...
$ non_linear_1: num [1:100] 0.372 -0.167 0.514 0.552 0.147 ...
$ non_linear_2: num [1:100] 0.6689 0.801 0.8555 0.0501 0.6744 ...
$ non_linear_3: num [1:100] 0.281 0.174 0.17 0.561 0.429 ...
$ linear_1 : num [1:100] -2.316 0.562 -0.784 -0.226 -1.587 ...
$ linear_2 : num [1:100] 0.363 1.411 1.368 -0.407 0.763 ...
$ .truth : num [1:100] 0.99145 0.00313 0.84924 1 0.00423 ...
“class”が、当該レコードが属するクラスを示すファクター変数で、class_1とclass_2のいずれかのレベルが格納されています。
他の変数はclass_1とclass_2のうちどちらに属するかを予測するための説明変数(の候補)ですが、実際にクラス分類に使用できるのはtwo_factor_1とtwo_factor_2で、他はクラスと無相関という設定になっています。 具体的には、two_factor_1とtwo_factor_2の主効果と交互作用および引数に指定したinterceptによるバイアス(intercept - 4 * two_factor_1 + 4 * two_factor_2 + 2 * two_factor_1 * two_factor_2)を主な要素として計算した値を、ロジスティック関数でclass_1確率に変換し、当該確率をもとにランダムでクラスを割り当てています。
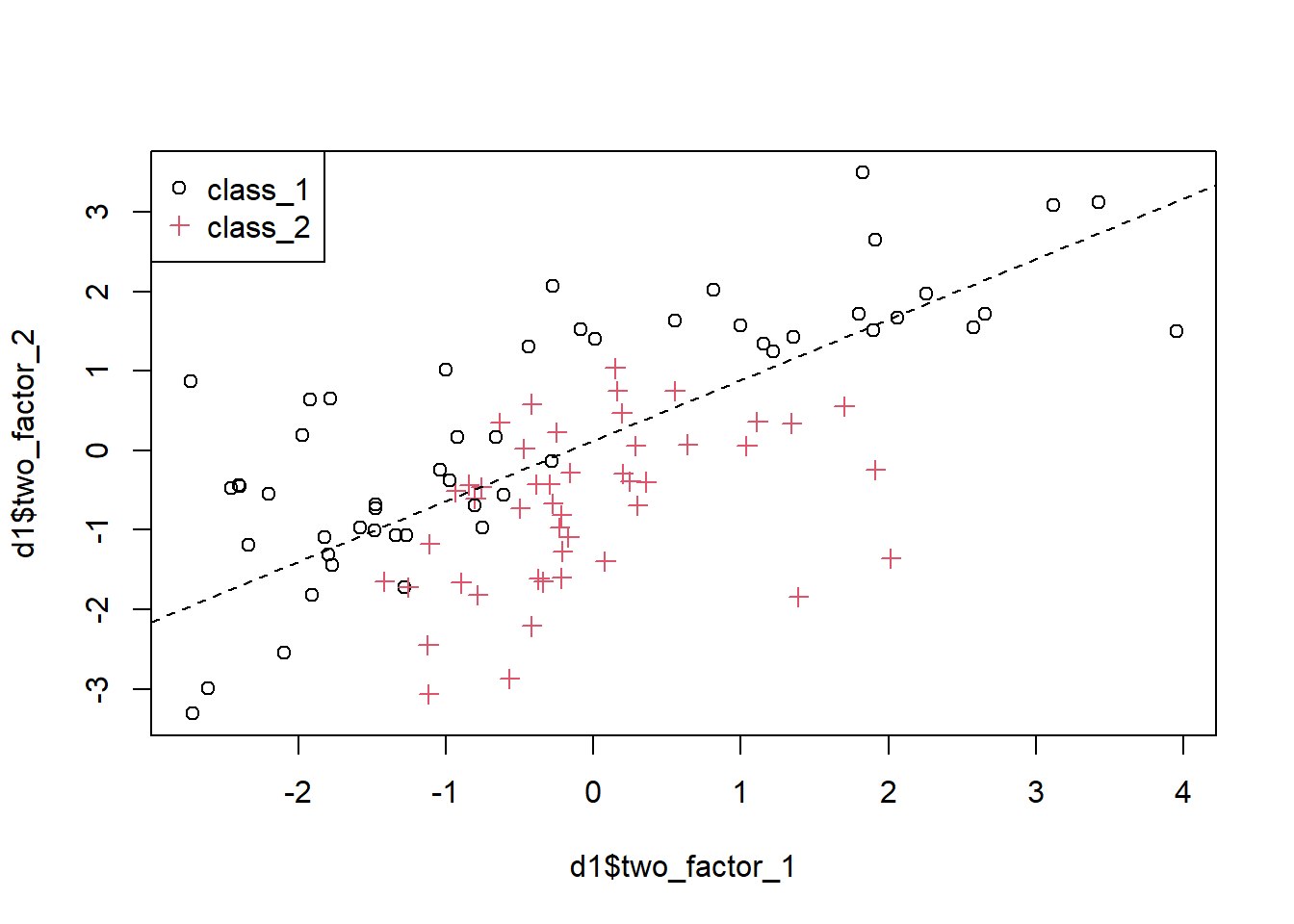
以下では生成したデータの分析イメージの参考例として、two_factor_1とtwo_factor2を使用して2クラスを分離する線形識別関数を求めています。 w_0+w_1*two\_factor\_1 + w_2*two\_factor\_2\geq0であればクラス1に、w_0+w_1*two\_factor\_1 + w_2*two\_factor\_2<0であればクラス2に分類するモデルを考えます。 教師データを、クラス1なら+1、クラス2なら-1として、最小二乗誤差基準により係数を推定しています。
# 線形識別関数のパラメータ推定
y <- ifelse(as.numeric(d1$class) > 1, -1, 1) # 教師データをclass_1=1, class_2=-1に変換
X <- cbind(1, as.matrix(d1[, c("two_factor_1", "two_factor_2")])) # パターン行列
w_hat <- solve(t(X) %*% X) %*% t(X) %*% y # 正規方程式で最小二乗法の解を求める
# 結果のplot
plot(x=d1$two_factor_1, y=d1$two_factor_2,
pch=ifelse(as.numeric(d1$class)==1, 1, 3),
col=d1$class)
legend("topleft", legend=levels(d1$class), pch=c(1, 3), col=c(1, 2))
abline(a=w_hat[1]/w_hat[3], b=-w_hat[2]/w_hat[3], lty=2)
sim_regression
sim_regression関数は、回帰用のシミュレーションデータを生成します。 以下の実行例の通り、目的変数outcomeとその数値の算出に使用した説明変数(predictor)が出力されます。
d2 <- sim_regression(
num_samples = 100, # 生成するレコード数(デフォルトは100)
method = "sapp_2014_1", # 生成方法(デフォルトは"sapp_2014_1")
std_dev = NULL, # 平均0の正規分布によるエラー項の標準偏差(デフォルトはNULLで、NULLの場合methodごとに決まった値が使用される)
factors = FALSE, # predictorに二値変数が含まれる場合のfactor化有無(デフォルトはFALSE)
keep_truth = TRUE # エラー項を含まない予測値の出力有無(デフォルトはFALSE)
)
str(d2)
tibble [100 × 22] (S3: tbl_df/tbl/data.frame)
$ outcome : num [1:100] 86.16 3.85 2.92 1.63 -29.98 ...
$ predictor_01: num [1:100] 0.9404 1.8374 -5.0732 2.3541 0.0358 ...
$ predictor_02: num [1:100] 1.365 4.276 -0.627 -3.694 -1.082 ...
$ predictor_03: num [1:100] -3.072 -4.163 -0.148 5.433 -0.299 ...
$ predictor_04: num [1:100] -8.62 -1.28 -4.46 1.77 -1.33 ...
$ predictor_05: num [1:100] -3.616 0.904 -4.617 1.906 2.109 ...
$ predictor_06: num [1:100] 0.34 -1.695 0.242 -2.087 -3.289 ...
$ predictor_07: num [1:100] -4.21 7.15 2.62 -4.61 3.4 ...
$ predictor_08: num [1:100] 3.15 1.1 5.92 1.34 -1.47 ...
$ predictor_09: num [1:100] -6.019 -4.679 5.888 -0.535 4.073 ...
$ predictor_10: num [1:100] 5.38 -4.09 -2.12 -1.67 -0.93 ...
$ predictor_11: num [1:100] -0.748 -3.666 -0.218 4.095 -1.373 ...
$ predictor_12: num [1:100] -1.35 4.332 -0.466 -3.065 4.615 ...
$ predictor_13: num [1:100] -1.597 -1.496 -3.45 0.379 1.419 ...
$ predictor_14: num [1:100] 3.372 2.093 0.543 -0.509 -0.704 ...
$ predictor_15: num [1:100] -2.921 -0.299 -0.332 3.577 -4.968 ...
$ predictor_16: num [1:100] -0.806 0.353 -2.567 6.526 -3.973 ...
$ predictor_17: num [1:100] 1.634 1.589 -2.139 0.177 -2.733 ...
$ predictor_18: num [1:100] -0.44 2.02 2.43 5.27 -3.65 ...
$ predictor_19: num [1:100] -2.093 0.054 -0.538 -1.95 -5.075 ...
$ predictor_20: num [1:100] -4.099 1.618 -3.966 -0.844 -6.315 ...
$ .truth : num [1:100] 80.258 5.973 4.227 0.864 -26.845 ...
predictorの数や生成方法、およびそれらのpredictorから目的変数outcomeを計算する算式は、method引数の指定により異なります。
上の実行例で指定した”sapp_2014_1”では、平均0、分散9の正規乱数を独立に20個生成してpredictorとし、以下コードに示す計算式の算出結果に正規分布に従うエラー項を加算してoutcomeを作成しています。
y <- with(d2,
# "sapp_2014_1"の算式
predictor_01 + sin(predictor_02) + log(abs(predictor_03)) +
predictor_04^2 + predictor_05 * predictor_06 +
ifelse(predictor_07 * predictor_08 * predictor_09 < 0, 1, 0) +
ifelse(predictor_10 > 0, 1, 0) + predictor_11 * ifelse(predictor_11 > 0, 1, 0) +
sqrt(abs(predictor_12)) + cos(predictor_13) + 2 * predictor_14 + abs(predictor_15) +
ifelse(predictor_16 < -1, 1, 0) + predictor_17 * ifelse(predictor_17 < -1, 1, 0) -
2 * predictor_18 - predictor_19 * predictor_20
)
# パッケージの計算結果との比較
head(data.frame(list(
.truth = d2$.truth,
check = y
)))
.truth check
1 80.2583408 80.2583408
2 5.9726707 5.9726707
3 4.2265011 4.2265011
4 0.8642132 0.8642132
5 -26.8451499 -26.8451499
6 -7.8300851 -7.8300851
バージョン1.4.0時点では、生成方法を指定するmethod引数として、“sapp_2014_1”以外にも”sapp_2014_2”、“van_der_laan_2007_1”および”van_der_laan_2007_2”が選択可能です。 それぞれの生成方法の詳細はリファレンス[2]をご参照ください。
sim_noise
sim_noise関数は平均0、分散1の正規分布に従う乱数を生成します。
d3 <- sim_noise(
num_samples = 10, # 生成するレコード数
num_vars = 3, # 生成するカラム(正規乱数)の数
cov_type = "exchangeable", # 分散共分散行列の設定(デフォルトは"exchangeable")
outcome = "none", # outcome変数の出力有無(デフォルトは"none")
num_classes = 2, # outcome="classification"の場合のクラス数(デフォルトは2)
cov_param = 0 # 変数間の共分散に関するパラメータ(デフォルトは0)
)
str(d3)
tibble [10 × 3] (S3: tbl_df/tbl/data.frame)
$ noise_1: num [1:10] 0.6842 0.5628 -0.0469 -1.1456 0.1879 ...
$ noise_2: num [1:10] 0.961 0.306 -0.15 0.465 -0.471 ...
$ noise_3: num [1:10] 2.11547 0.80998 -0.00872 0.16157 -0.91603 ...
各レコードはnoise_iとしてnum_varsで指定した数だけ変数が生成されていますが、これらは多変量正規分布に従っています。 この多変量正規分布は、前述のとおり平均は0、分散共分散行列の対角成分(分散)は1に固定されていますが、変数間の共分散は引数cov_typeとcov_paramで制御します。 cov_type=“exchangeable”を指定すると、どの(異なる)変数間の共分散もcov_paramで設定した値になります。 一方、cov_type=“toeplitz”では、cov_paramで指定した値から、変数間のインデックスが離れるにつれて共分散が指数的に変化するような行列となります。(例えば、noise_1とnoise_2間の共分散がcov_param=0.5とすると、noise_1とnoise_3間の共分散は0.5^2=0.25、noise_1とnoise_4間の共分散は0.5^3=0.125等となります。)
引数outcomeに”regression”または”classification”を指定すると、それぞれ数値変数及びクラスを示すファクター変数が出力されますが、いずれも変数noise_iとは関連のない、ランダムな値が設定されます。
sim_logistic、sim_multinomial
sim_logistic関数及びsim_multinomial関数は、それぞれ2クラス分類および3クラス分類用のデータを生成します。 平均0、分散1、相関係数が引数correlationに従う正規乱数AおよびBの2変数を説明変数として使用しますが、クラス確率を計算するためのAとBの算式を、柔軟に設定できる点が特徴です。
以下はsim_logistic関数による実行例です。 引数eqnには”~“から始まる2変数AとBの式、すなわち右辺のみのformulaオブジェクトを指定します。 eqnで指定した数式で計算した値をロジスティック関数によりクラス1確率に変換し、当該確率をもとにランダムにクラスを割り当てています。
d4 <- sim_logistic(
num_samples = 1000, # 生成するレコード数
eqn = ~ 2 * A + B^2 + 1.2, # 2つの正規乱数AとBにより予測子を計算する算式
#eqn = rlang::expr(2 * A + B^2 + 1.2), # 参考:expressionで指定することも可能
#eqn = base::expression(2 * A + B^2 + 1.2)[[1]], # 参考:expression listは指定できないため注意
correlation = 0, # 変数AとBの相関係数(デフォルトは0)
keep_truth = TRUE # クラス1確率の出力有無(デフォルトはFALSE)
)
str(d4)
tibble [1,000 × 5] (S3: tbl_df/tbl/data.frame)
$ A : num [1:1000] 0.104 1.375 -2.597 0.526 -1.029 ...
$ B : num [1:1000] -0.858 -1.359 0.397 0.504 1.75 ...
$ .linear_pred: num [1:1000] 2.15 5.8 -3.84 2.5 2.21 ...
$ .truth : num [1:1000] 0.8953 0.997 0.0211 0.9245 0.9008 ...
$ class : Factor w/ 2 levels "one","two": 1 1 2 1 1 1 1 2 1 1 ...
# クラス確率が指定した式に従って算出されていることの確認
p <- 1 / (1 + exp(-(2*d4$A + d4$B^2 + 1.2)))
head(data.frame(list(
.truth = d4$.truth,
check = p
)))
.truth check
1 0.8952554 0.8952554
2 0.9969767 0.9969767
3 0.0211242 0.0211242
4 0.9244752 0.9244752
5 0.9008286 0.9008286
6 0.9437250 0.9437250
sim_multinomial関数は、3クラス分類用のデータを生成します。
説明変数はsim_logistic関数と同様、正規分布に従う乱数AとBの二つですが、AとBの算式として、三つのクラスに対応する三つの式eqn_1~eqn_3を指定します。 これら三つの式の算出結果を入力とするソフトマックス関数P(class=k)=exp(eqn\_k)/\Sigma_{i}{exp(eqn\_i)}により各クラスのクラス確率を計算し、当該確率をもとに、ランダムに3クラスのいずれかを割り当てています。
d5 <- sim_multinomial(
num_samples = 10, # 生成するレコード数
eqn_1 = ~ A + B, # クラス1に対応する式
eqn_2 = ~ 2 * A * B, # クラス2に対応する式
eqn_3 = ~ log(abs(B)), # クラス3に対応する式
correlation = 0, # 変数AとBの相関係数(デフォルトは0)
keep_truth = TRUE # 各クラスのクラス確率の出力有無(デフォルトはFALSE)
)
str(d5)
tibble [10 × 6] (S3: tbl_df/tbl/data.frame)
$ A : num [1:10] -1.236 0.668 -1.119 0.173 0.375 ...
$ B : num [1:10] 0.184 1.404 0.44 0.216 -0.84 ...
$ class : Factor w/ 3 levels "one","two","three": 1 1 1 2 1 3 2 2 1 2
$ .truth_one : num [1:10] 0.299 0.5 0.384 0.533 0.314 ...
$ .truth_two : num [1:10] 0.543 0.411 0.283 0.389 0.266 ...
$ .truth_three: num [1:10] 0.158 0.0885 0.3331 0.0779 0.4196 ...
# クラス確率が指定した式に従って算出されていることの確認
## 引数で指定した三つの算式
y1 <- d5$A + d5$B
y2 <- 2 * d5$A * d5$B
y3 <- log(abs(d5$B))
## ソフトマックス関数によるクラス確率
p1 <- exp(y1) / (exp(y1) + exp(y2) + exp(y3))
p2 <- exp(y2) / (exp(y1) + exp(y2) + exp(y3))
p3 <- exp(y3) / (exp(y1) + exp(y2) + exp(y3))
## パッケージによる計算結果と比較
head(data.frame(list(
.truth_one = d5$.truth_one,
check_one = p1,
.truth_two = d5$.truth_two,
check_two = p2,
.truth_three = d5$.truth_three,
check_three = p3
)))
.truth_one check_one .truth_two check_two .truth_three check_three
1 0.2991672 0.2991672 0.5428603 0.5428603 0.15797249 0.15797249
2 0.5003462 0.5003462 0.4111912 0.4111912 0.08846260 0.08846260
3 0.3839573 0.3839573 0.2829503 0.2829503 0.33309237 0.33309237
4 0.5328413 0.5328413 0.3892420 0.3892420 0.07791673 0.07791673
5 0.3140786 0.3140786 0.2662960 0.2662960 0.41962537 0.41962537
6 0.5666486 0.5666486 0.3759692 0.3759692 0.05738220 0.05738220