shapviz

Author

データサイエンス関連基礎調査WG

Published

August 1, 2025

パッケージの概要

shapvizは、予測モデルの解釈手法の一種であるSHAPの可視化に特化したパッケージです。 treeshapやkernelshap等のSHAPを計算するパッケージと組み合わせて使用します。

SHAPとは

SHAPという手法については データサイエンス関連基礎調査WG　大江麗地 (2024) に解説があるため、こちらを参照することをお勧めします。 以下では詳細な説明は避け、概要のみを記載します。

SHAP(SHapley Additive exPlanation)とは予測モデルの解釈に用いられる手法の一種で、 ある予測モデルの入力（説明変数）と出力（予測値）の組に対して、 どの説明変数の寄与によってその予測値となったのかを加法的に分解するものです。

個別の予測値 = その予測の説明変数1の寄与 + \cdots + その予測の説明変数Nの寄与 + 予測値平均

このようにして分解された各サンプル・説明変数の寄与をSHAP値と呼びます。

個別サンプルの予測に対する解釈を与える、いわゆるローカルな手法だと考えられますが、 多くのサンプルのSHAPを計算してそれをグラフにする、平均値で要約する等により、 モデル全体の解釈を与える、いわゆるグローバルな手法としても使用することが出来ます。

準備

パッケージの読み込み

library(AER) #データセット

library(tibble) #data.frame拡張版
library(dplyr) #data.frameの操作
library(rsample) #データ分割
library(recipes) #前処理

library(xgboost) #今回使用するモデルのパッケージ
library(ROCR) #精度評価
library(treeshap) #SHAPの計算

library(ggplot2) #グラフの描画
library(patchwork) #複数のgpplotを組み合わせる
library(shapviz) #SHAPの可視化

データセットの読み込み

Christian Kleiber and Achim Zeileis (2008) で使用されたデータセット等をまとめたパッケージAERに含まれる、 HealthInsuranceというデータセットを使用します。

性別・年齢・学歴・家族構成・雇用状態（自営業か否か）健康保険の加入状況等に関する 約9,000個のサンプルが含まれています。 今回は、健康保険に加入しているかどうかを予測するモデルを作成することとします。

データセットの詳細については Achim Zeileis (2024) を参照してください1。

data("HealthInsurance")
df_all <- HealthInsurance

summary(df_all)
 health          age        limit         gender     insurance  married   
 no : 629   Min.   :18.00   no :7571   female:4169   no :1750   no :3369  
 yes:8173   1st Qu.:30.00   yes:1231   male  :4633   yes:7052   yes:5433  
            Median :39.00                                                 
            Mean   :38.94                                                 
            3rd Qu.:48.00                                                 
            Max.   :62.00                                                 
                                                                          
 selfemp        family             region     ethnicity         education   
 no :7731   Min.   : 1.000   northeast:1682   other: 365   none      :1119  
 yes:1071   1st Qu.: 2.000   midwest  :2023   afam :1083   ged       : 374  
            Median : 3.000   south    :3075   cauc :7354   highschool:4434  
            Mean   : 3.094   west     :2022                bachelor  :1549  
            3rd Qu.: 4.000                                 master    : 524  
            Max.   :14.000                                 phd       : 135  
                                                           other     : 667

前処理

今回例として使用するモデルでは、説明変数が数値型である必要があるので、factor型変数を数値型に変換しておきます2。

rec_init <- df_all %>% recipe(insurance ~ .) %>% #前処理手順の定義
  #ethinicityは最も多いカテゴリがcaucなので、これを基準カテゴリに変更
  step_relevel(ethnicity, ref_level = "cauc") %>% 
  #educationは学歴を表す説明変数で、大きいほど高学歴であるため、そのままダミー変数にするのではなく、数値に変換
  step_mutate(education_main = as.numeric(education) - 1) %>%
  #ただし、最後のカテゴリだけは「その他」を表しているので、これだけは別のダミー変数に分離する
  step_mutate(education_other = if_else(education_main == 6, 1, 0)) %>%
  step_mutate(education_main = if_else(education_main < 6, education_main, 0)) %>%
  step_rm(education) %>%
  step_dummy(all_factor_predictors()) %>% #他のfactor型変数は単純にダミー変数化
  step_relevel(insurance, ref_level = "yes")
  #目的変数は健康保険に加入しているかを表すinsurance

df_baked <- rec_init %>% prep() %>% bake(new_data = NULL) #上記で定義した前処理手順を実際に実行

上記前処理を施したうえで、学習データとテストデータに分割します。

set.seed(2024)
split_df <- rsample::initial_split(df_baked, prop = 0.8) #80%を学習データ、20%をテストデータとする
df_train <- rsample::training(split_df)
df_test <- rsample::testing(split_df)

df_train_x <- df_train %>% dplyr::select(-insurance)
df_train_y <- df_train$insurance
df_test_x <- df_test %>% dplyr::select(-insurance)
df_test_y <- df_test$insurance

モデル構築

続いてXGBoostによる予測モデルを学習データをもとに構築します。3

2値分類の問題ですが、予測モデルの出力としては加入しているか否かの2通りではなく、 加入している確率を出力するようにしています。

set.seed(2024)
model_xgboost <- xgboost(data = as.matrix(df_train_x), label = as.matrix(2 - as.numeric(df_train_y)), nrounds = 100,
                  params = list(eta = 0.3, max_depth = 2, gamma = 0, min_child_weight = 1, 
                             subsample = 1, colsample_bytree = 1, colsample_bynode = 2/14, objective = "binary:logistic"),
                  verbose = 0)

構築した予測モデルの精度をテストデータを用いて確認しておきます。

ここではAUC(ROC)を確認します。これは2値分類モデルで使用される評価指標で、高いほど精度が良いという評価になります。

calc_score <- function(object, predfun, df_test_x, df_test_y){
  yhat <- object %>% predfun(df_test_x)
  pr <- ROCR::prediction(yhat, df_test_y)
  auc <- pr %>% ROCR::performance("auc")
  auc_plot <- pr %>% ROCR::performance("tpr", "fpr")
  list(
    auc_plot = auc_plot,
    auc = auc@y.values %>% as.numeric()
    )
}

predfun_xgboost <- function(object, newdata){
  dt <- as.matrix(newdata)
  object %>% predict(newdata = dt)
}
score <- calc_score(model_xgboost, predfun_xgboost, df_test_x, df_test_y)
score$auc_plot %>% plot()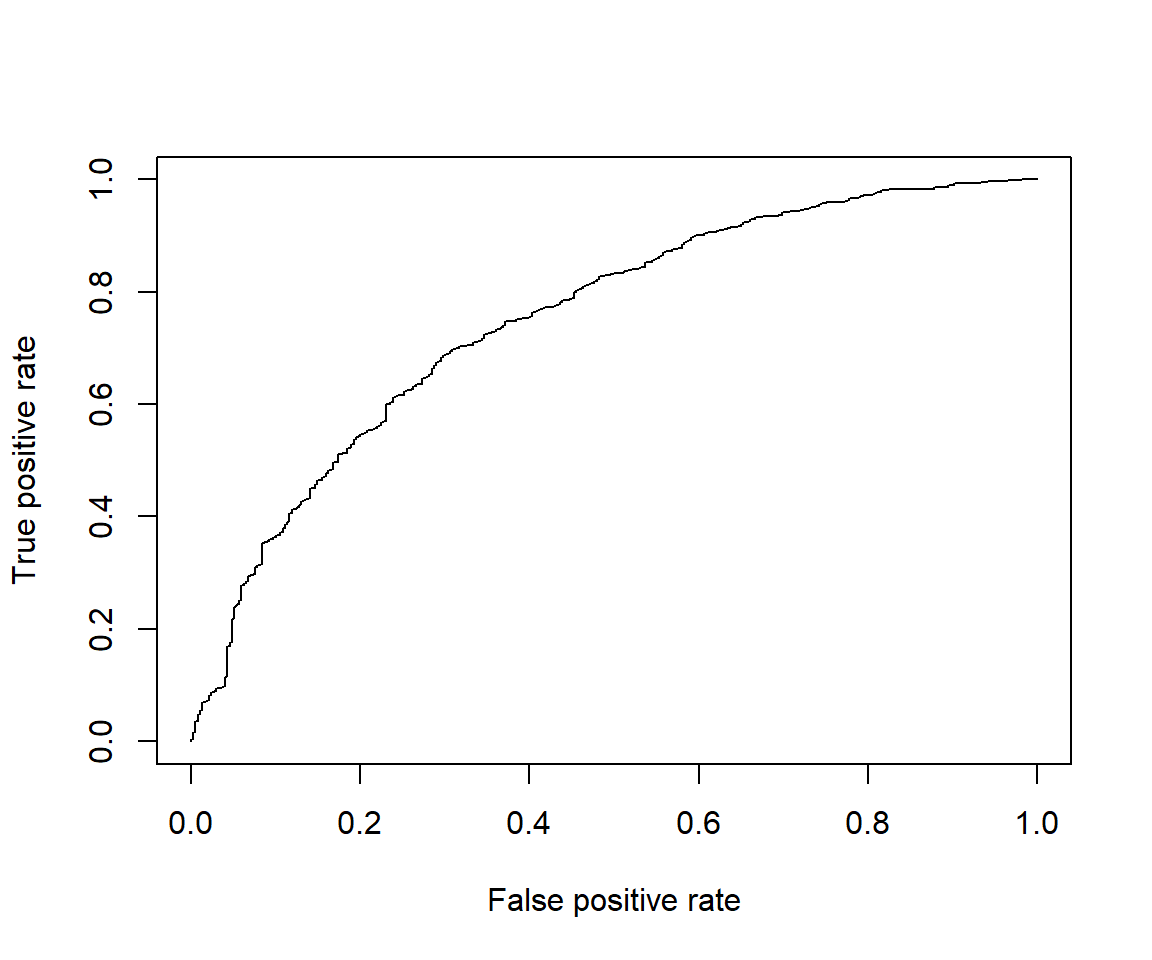

score$auc
[1] 0.7503933

0.75は高くもなく低くもないといった程度ではあるものの、用途によってはこれでも十分でしょう。 （例えば True Positive Rate = 0.6, False Positive Rate = 0.2 あたりとなるしきい値をとれば、 　全体の8割程度を占める加入者のうち6割を削減しつつ、少数派の非加入者のうち8割を残した集団が作れる） 　

基本的な使用方法

まずは別のパッケージを用いてSHAPを計算します。 ここでは計算が高速なtreeshapを使用します。

set.seed(2024) #SHAPを計算したいサンプル
nrow_shap <- nrow(df_train) #SHAPは計算コストが高いことが多いが、treeshapであれば全サンプルでも問題ない
df_shap <- df_train[sample(nrow(df_train), nrow_shap), ]
df_shap_x <- df_shap %>% dplyr::select(-insurance)

t1 <- proc.time()

obj_uni <- treeshap::unify(model_xgboost, df_shap_x)
shap_ts <- treeshap::treeshap(obj_uni, x = df_shap_x)

t2 <- proc.time()
t0 <- (t2-t1)[3]
names(t0) <- NULL

cat("処理時間:", t0, "秒")
処理時間: 0.44 秒

次に、shapviz関数でshapvizパッケージで可視化できるオブジェクトに変換します。

sv <- shapviz::shapviz(shap_ts)

最後に、このオブジェクトをshapvizパッケージの関数に入力することで可視化できます。 例えば、個別のサンプルに対する寄与の分解を表示するには次のようにします。

shapviz::sv_waterfall(sv, row_id = 1) #1つ目のサンプルの予測結果に対してプロット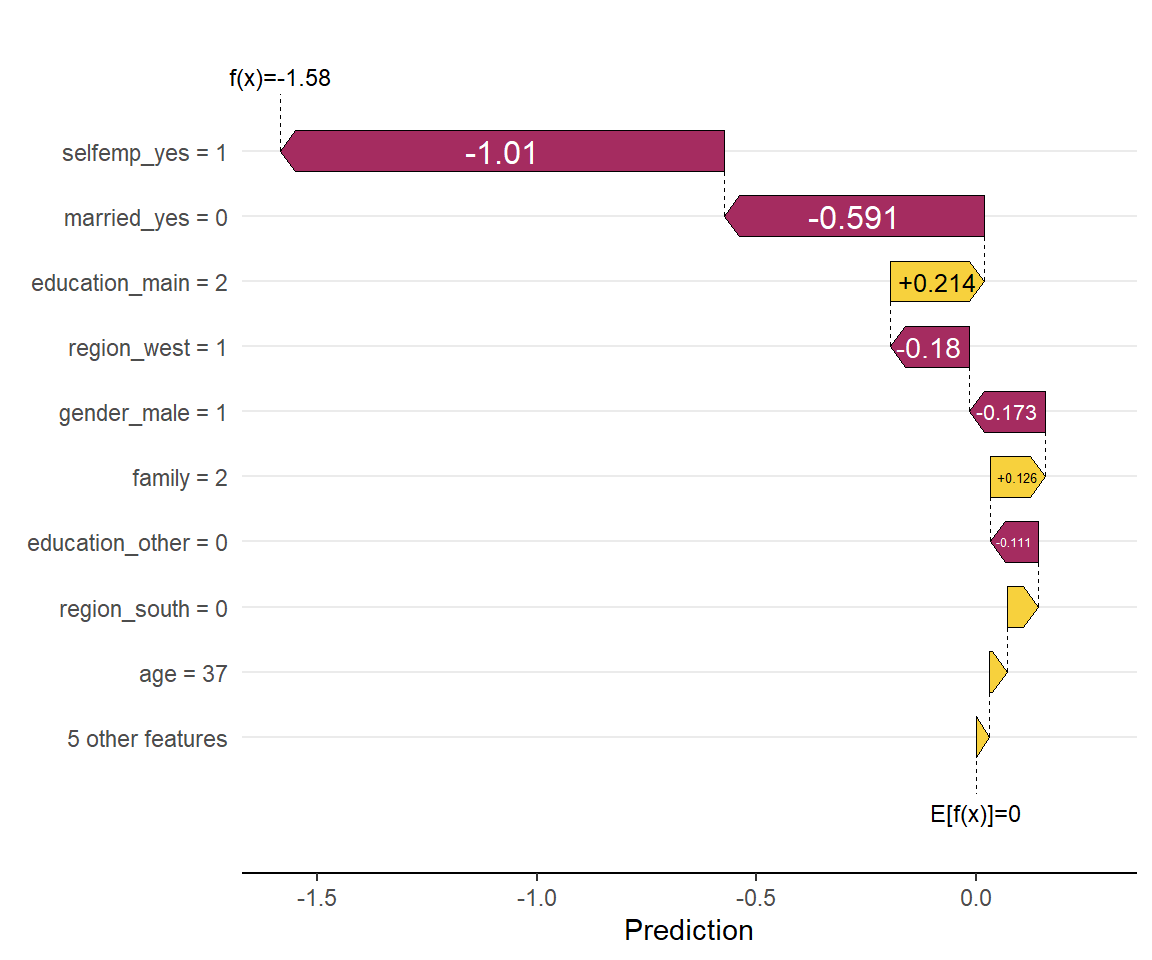

このサンプルでは、自営業であること（selfemp_yes=1）や独身である（married_yes=0）ことによって、 平均的な被験者よりも健康保険に加入しない傾向にあると判断されたようです。

上記sv_waterfallの他にも可視化を行う関数が色々用意されていますが、基本的な使用方法は同様です。

可視化方法一覧

SHAP Summary Plot

グローバルな手法として全サンプルの結果を一覧に表示し、 説明変数ごとに全般的にどの程度寄与しているかをプロットするには次のようにします。

shapviz::sv_importance(sv, kind = "beeswarm")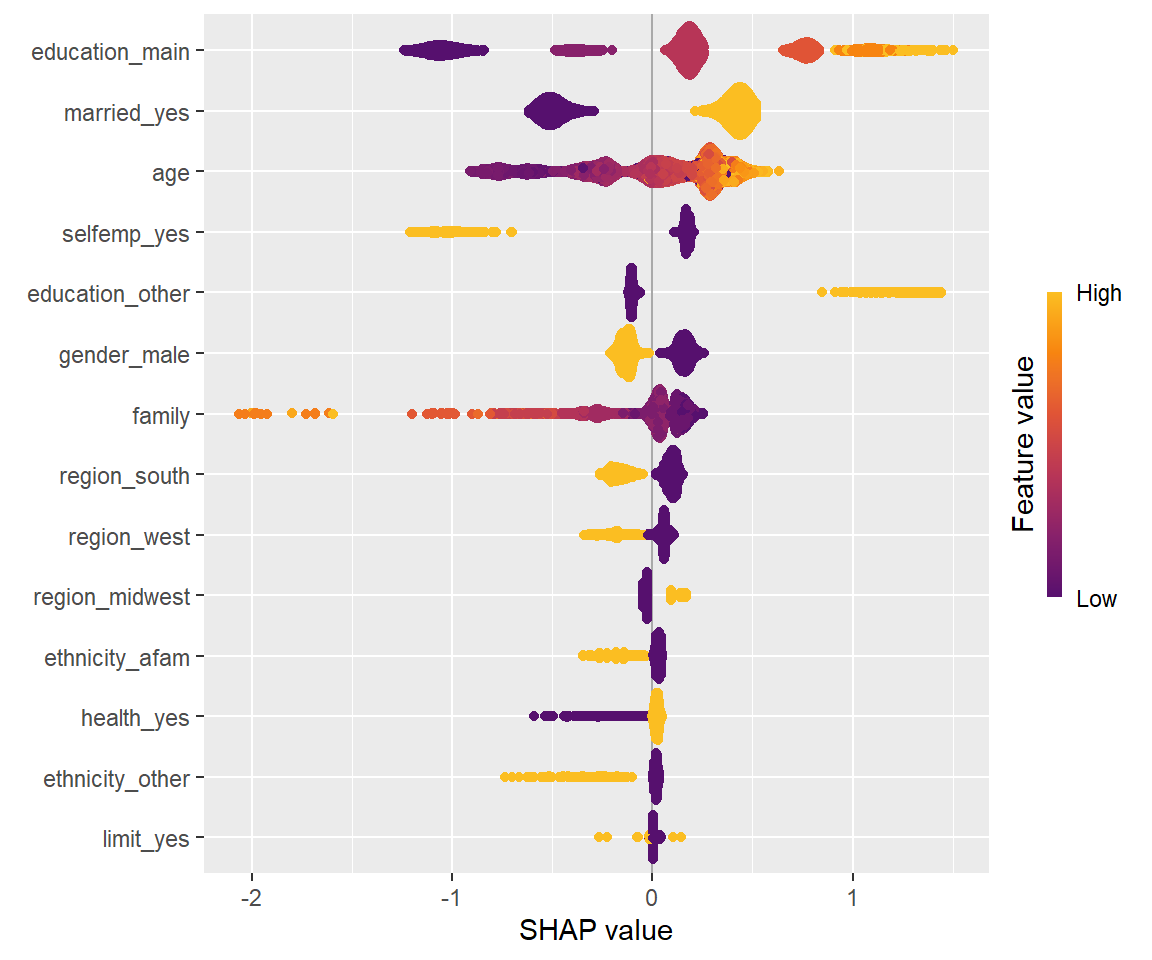

横軸は寄与の大きさを、色付けは説明変数の値を示しており、 例えば明るい色の点が右側にある場合は、その説明変数が高いほど予測確率が高くなることを示します。

デフォルトでは寄与が大きい説明変数から順に並べられるので、 最も予測確率への寄与が大きい説明変数は学歴（education_main）であることがわかります。 また、学歴が高いほど健康保険に加入する傾向があることがわかります。

SHAP Feature Importance Plot

Summary Plotは各サンプルの寄与をすべてプロットしていました。

寄与の絶対値の大きいサンプルが多い説明変数は重要であると考えられるので、 その平均値を棒グラフにして描画することで、どれが重要な説明変数なのかが一目でわかるようになります。

このようなプロットをFeature Importance Plot（特徴量重要度プロット）といい、プロットするには次のようにします。

shapviz::sv_importance(sv)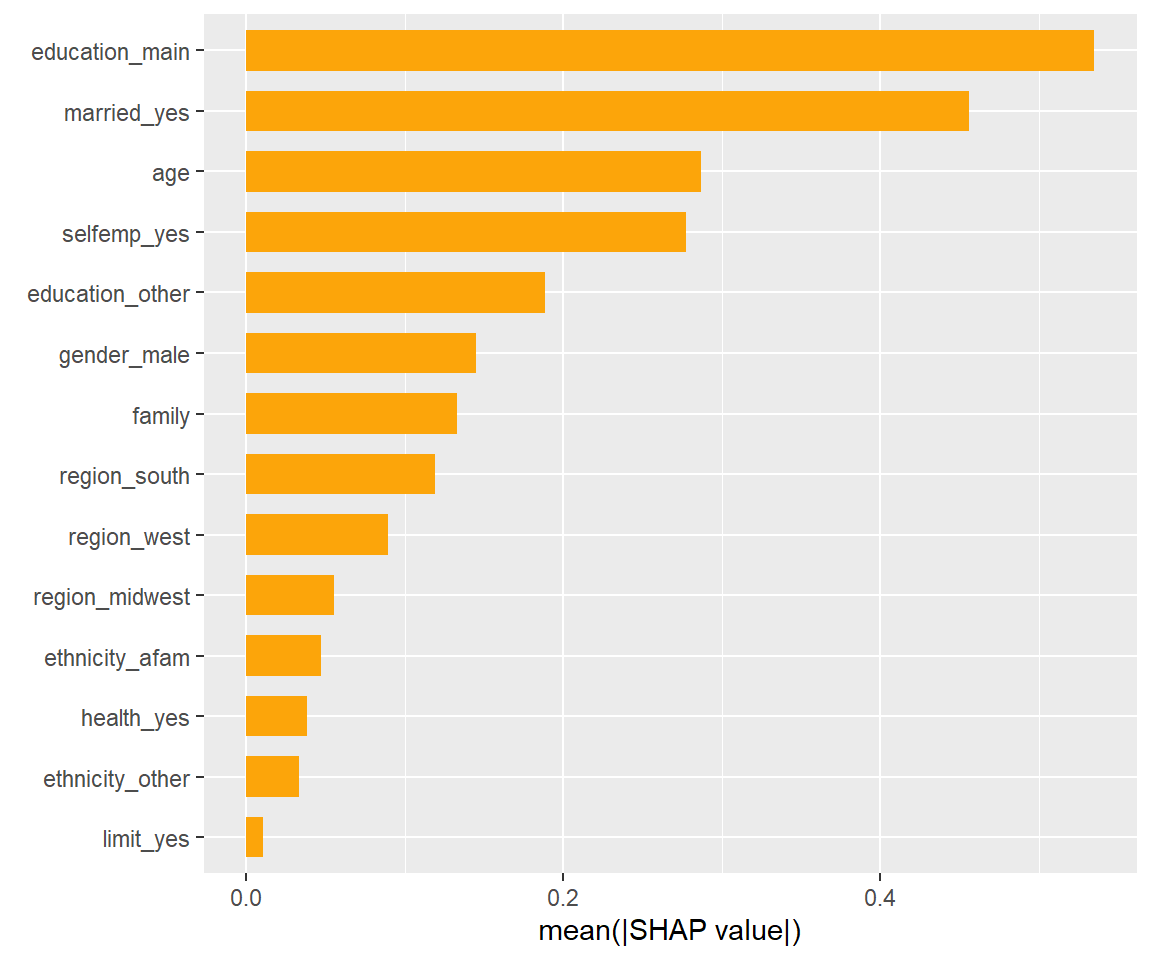

SHAP Dependence Plot

ここまでは説明変数の寄与の大きさを比較することを主目的としていました。 各説明変数に着目して、それがどのように寄与しているかはSummary Plotでも確認可能ですが、 横軸に説明変数の値、縦軸に寄与としたグラフをプロットすることも考えられます。

これをDependence Plotといい、プロットするにはsv_dependence関数を使用します。

shapviz::sv_dependence(sv, v = c("education_main", "age"), color_var = NULL)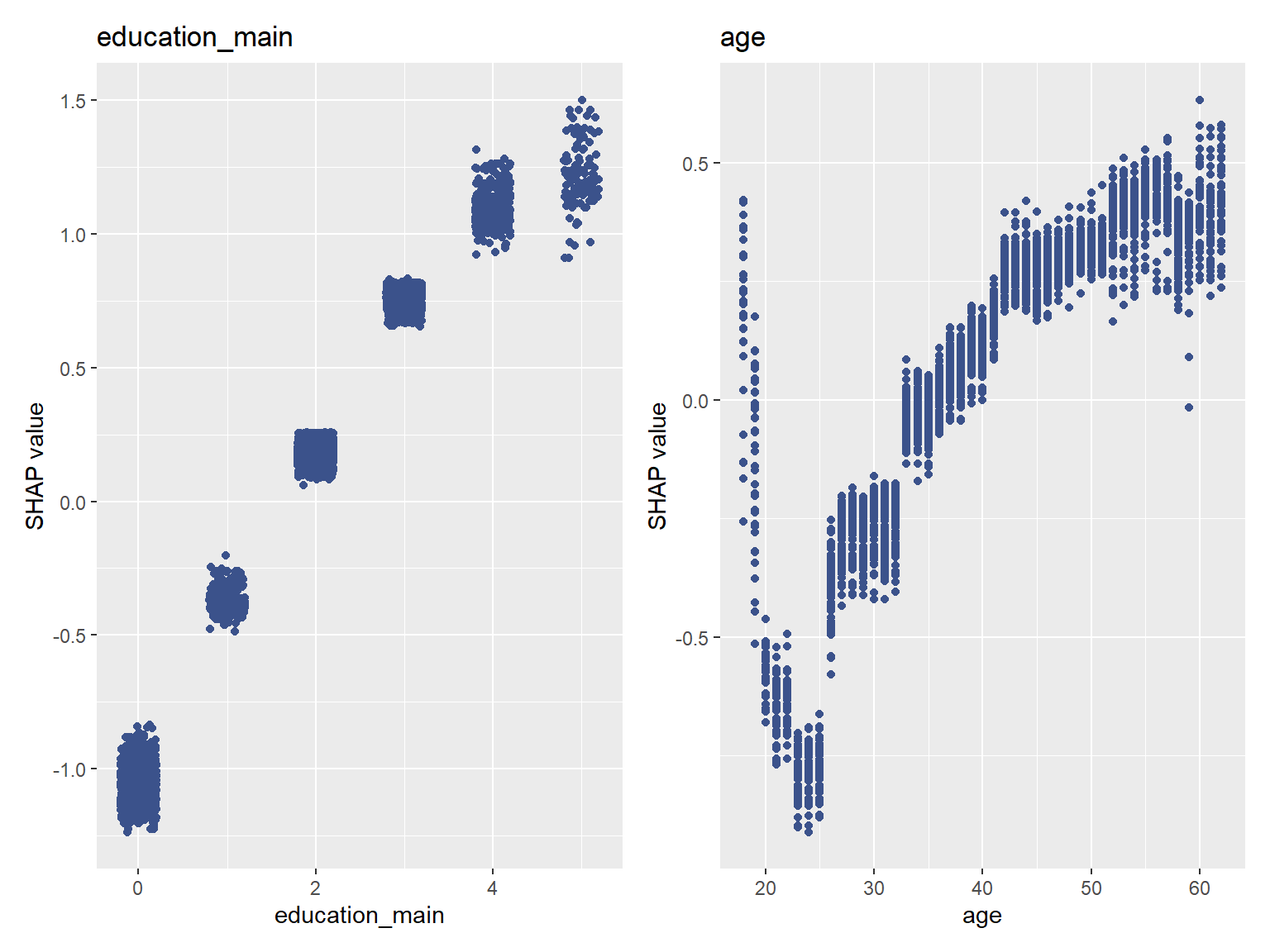

学歴がおおむね線形に影響を及ぼすことはSummary Plotでも大まかには確認できましたが、このようなグラフにすることでより明確になりました。 また、年齢が与える影響は非常に複雑で、20代前半で一度加入率が落ち込み、以降は少しずつ上がっていくという推移になることがわかります。

このプロットでは横軸が同じでも、縦軸（寄与）が異なる点が多数描かれています。 これはサンプルによって寄与が異なるためで、交互作用がある場合にこのような現象が発生します。

引数color_varを省略するか"auto"とすることで、交互作用の大きい説明変数を自動で選び、その値によってグラフが色分けされるようになります。

shapviz::sv_dependence(sv, v = c("education_main", "age"), color_var = "auto")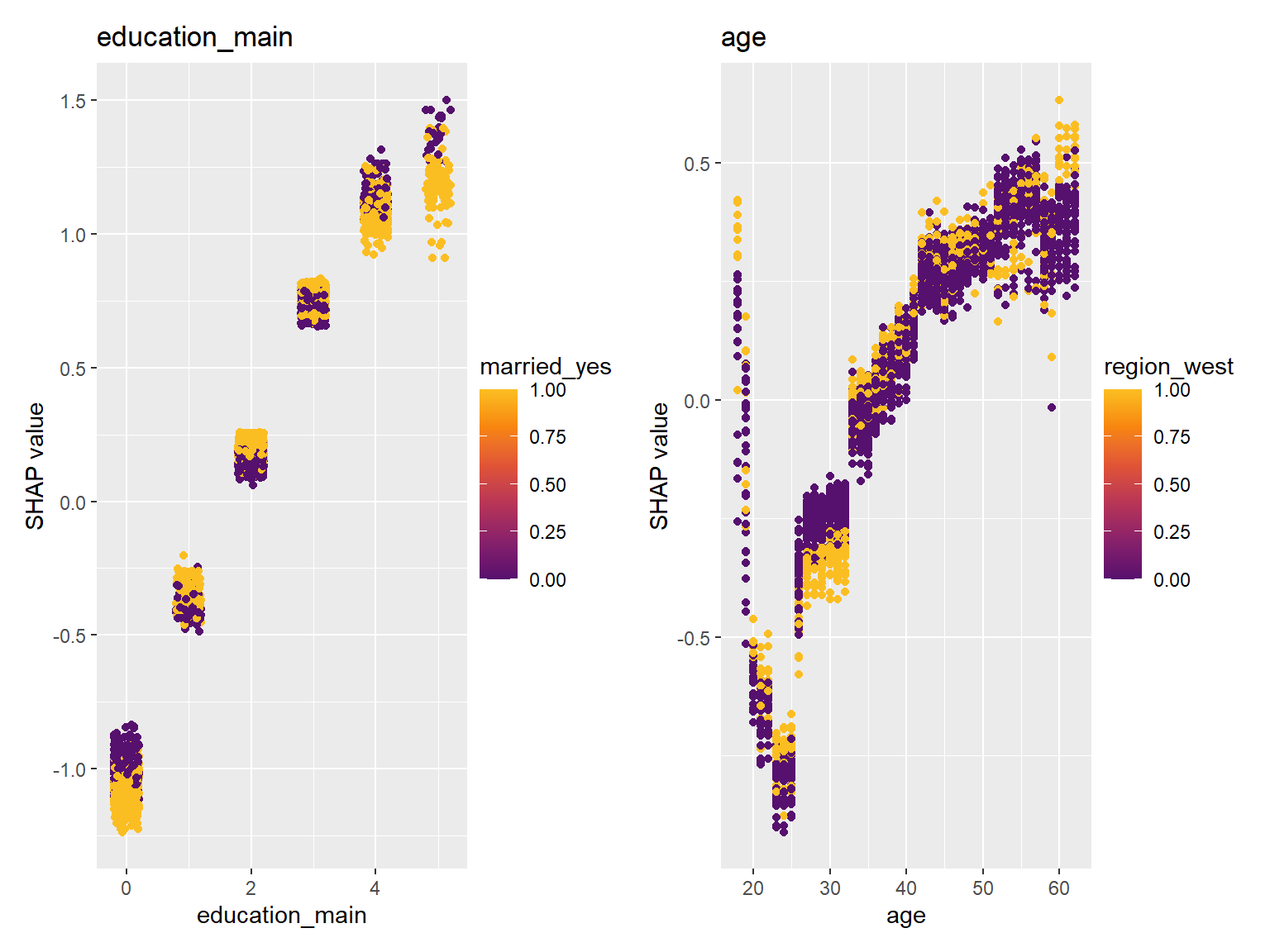

  • 学歴（education_main）と交互作用のある説明変数としては婚姻状況（married_yes）が選ばれました。 高卒・大卒（education_mainが1～3）では結婚している場合は若干SHAP値が上がる一方、それ以外の場合はその逆となるようです。 ややこしい話ですが、婚姻状況（married_yes）のSHAP値が、結婚している場合に正であるという状況はどのサンプルでも変わらないので、 結婚による加入率上昇はどの学歴層でもみられるものの、その効果は学歴によって差があるということになります。
  • 年齢（age）と交互作用のある説明変数としては、居住地域が西側であるかどうか（region_west）が選ばれました。 全体的な形はあまり変わらないように思われますが、居住地域が西側の場合、30歳前後での加入率が下がるようです。

引数color_varに説明変数名を指定することで、好きな特徴量で色分けをすることができます。

shapviz::sv_dependence(sv, v = "age", color_var = "married_yes")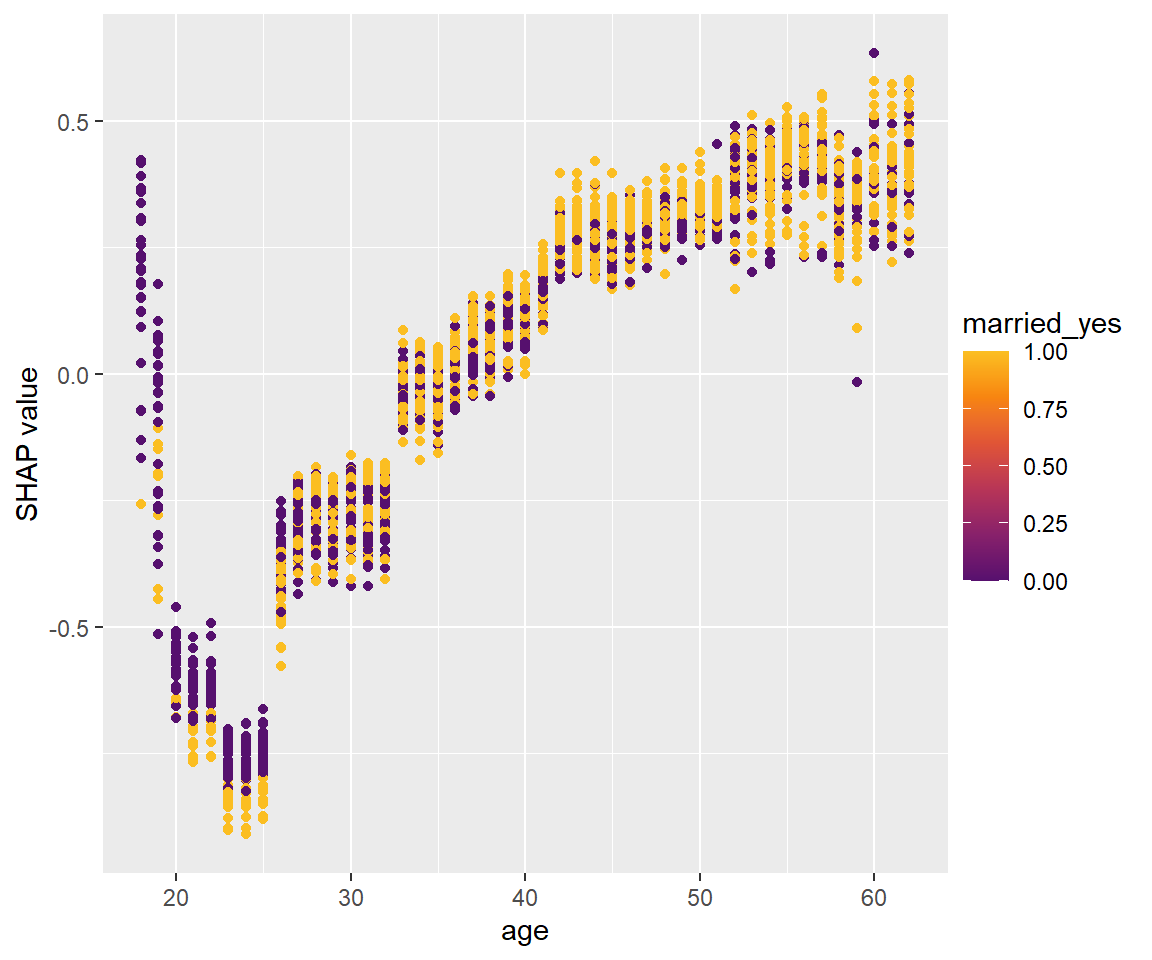

20代前半では結婚している（married_yes=1）と健康保険への加入率が低いように見える一方、それより上の年代では大きく差はないように見えます。

2D SHAP Dependence Plot

前述のSHAP Dependence Plotでは2つの説明変数の関係を色分けで示していましたが、 別の方法として縦軸と横軸に説明変数をとる方法もあります。使用する関数はsv_dependence2D関数です。 ここで色分けに使用されるSHAP値は2変数のSHAP値の合計になります。

shapviz::sv_dependence2D(sv, x = "education_main", y = "married_yes")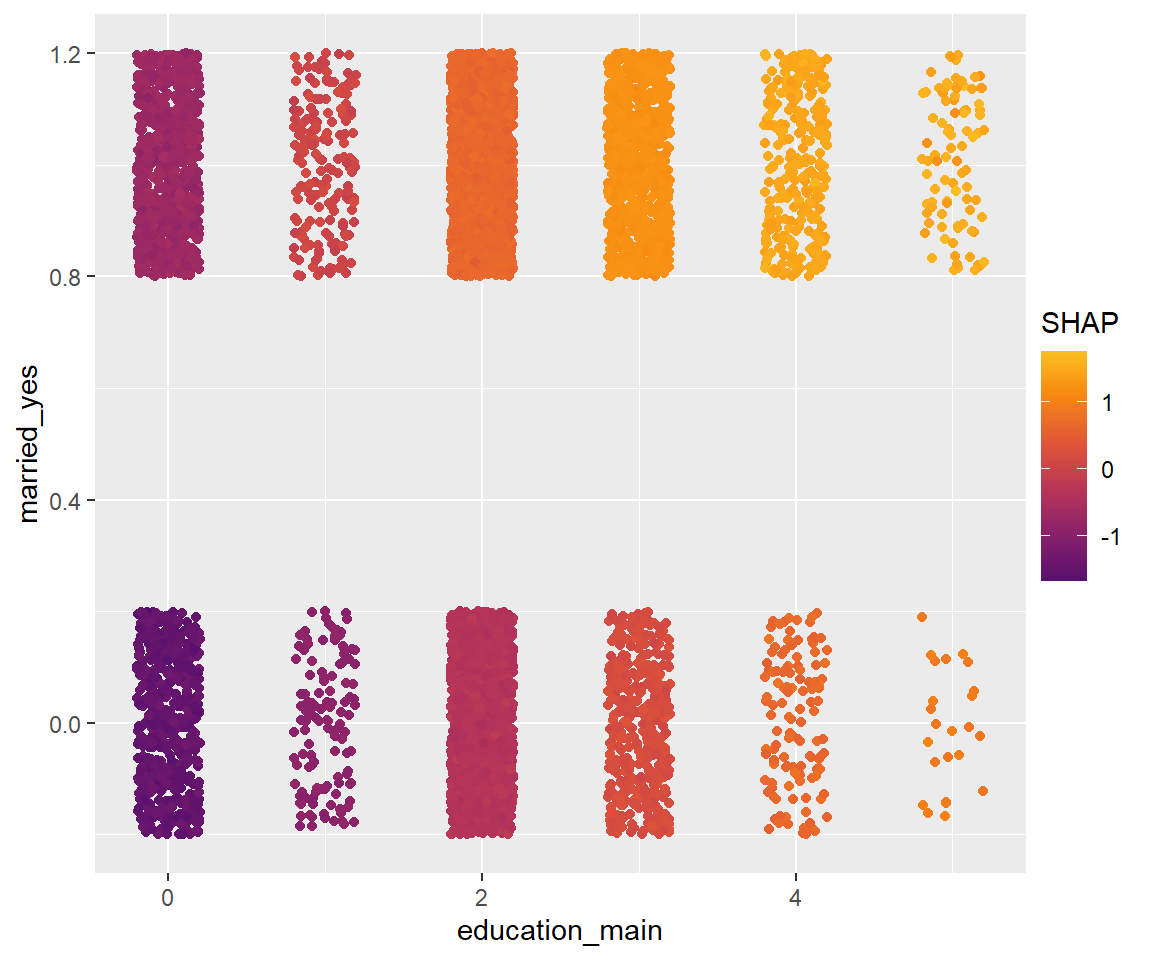

横軸（学歴）をどこにとっても、下側（独身）よりも上側（既婚）のほうが色が明るく、 前述した、「結婚による加入率上昇はどの学歴層でもみられる」という状況をうまく可視化することが出来ました。

なお、説明変数が地理データである場合には、 例えば横軸に経度、縦軸に緯度を取るような使い方もあります(Michael Mayer and Adrian Stando 2024a)。

SHAP Waterfall Plot

最初に例として挙げた、個別のサンプルに対する寄与の分解4をWaterfall Plotといいます。

shapviz::sv_waterfall(sv, row_id = 1) #1つ目のサンプルの予測結果に対してプロット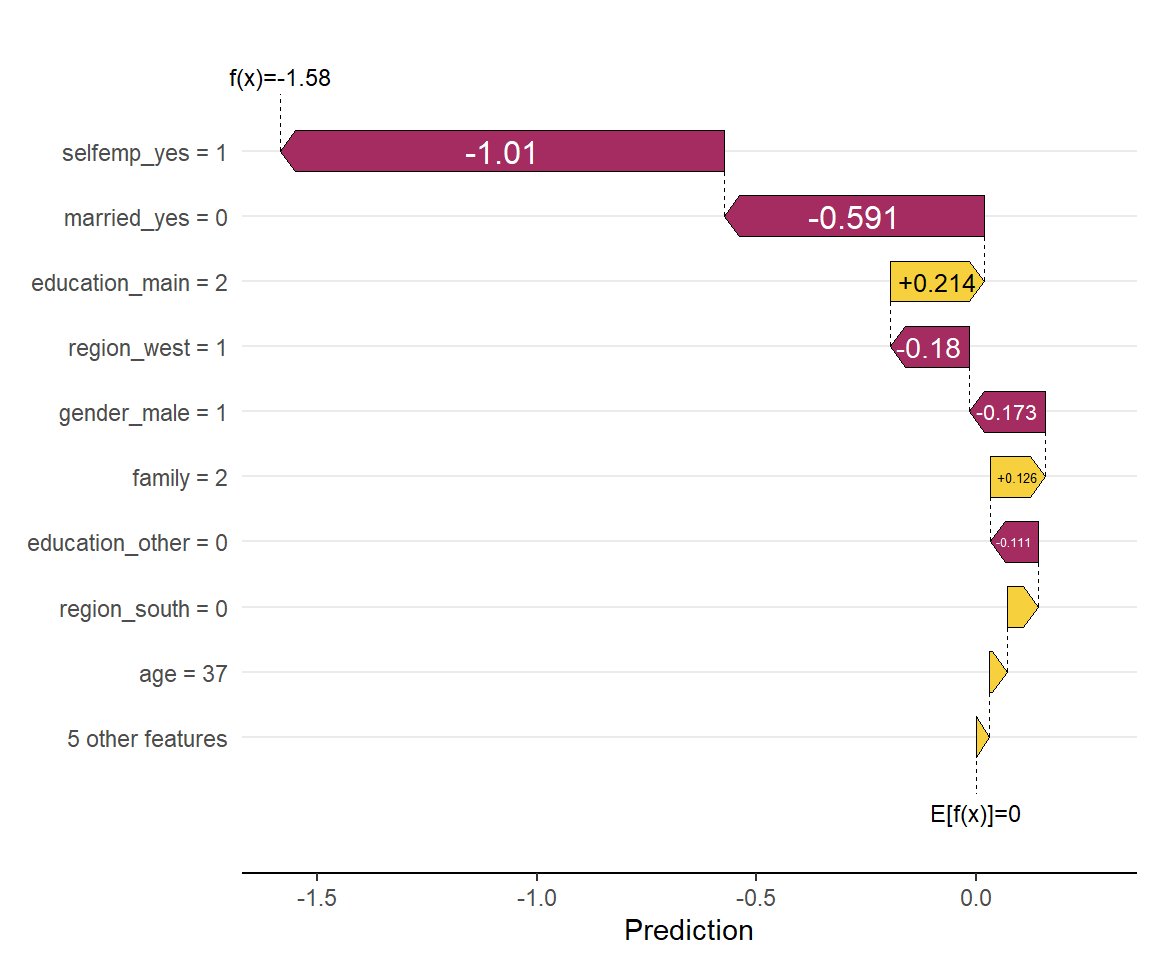

SHAP Force Plot

個別サンプルに対する寄与の分解についてはもう一つプロットが用意されており、 それが左側に正方向の寄与、右側に負方向の寄与を一次元的に並べるForce Plotです。

shapviz::sv_force(sv, row_id = 1) #1つ目のサンプルの予測結果に対してプロット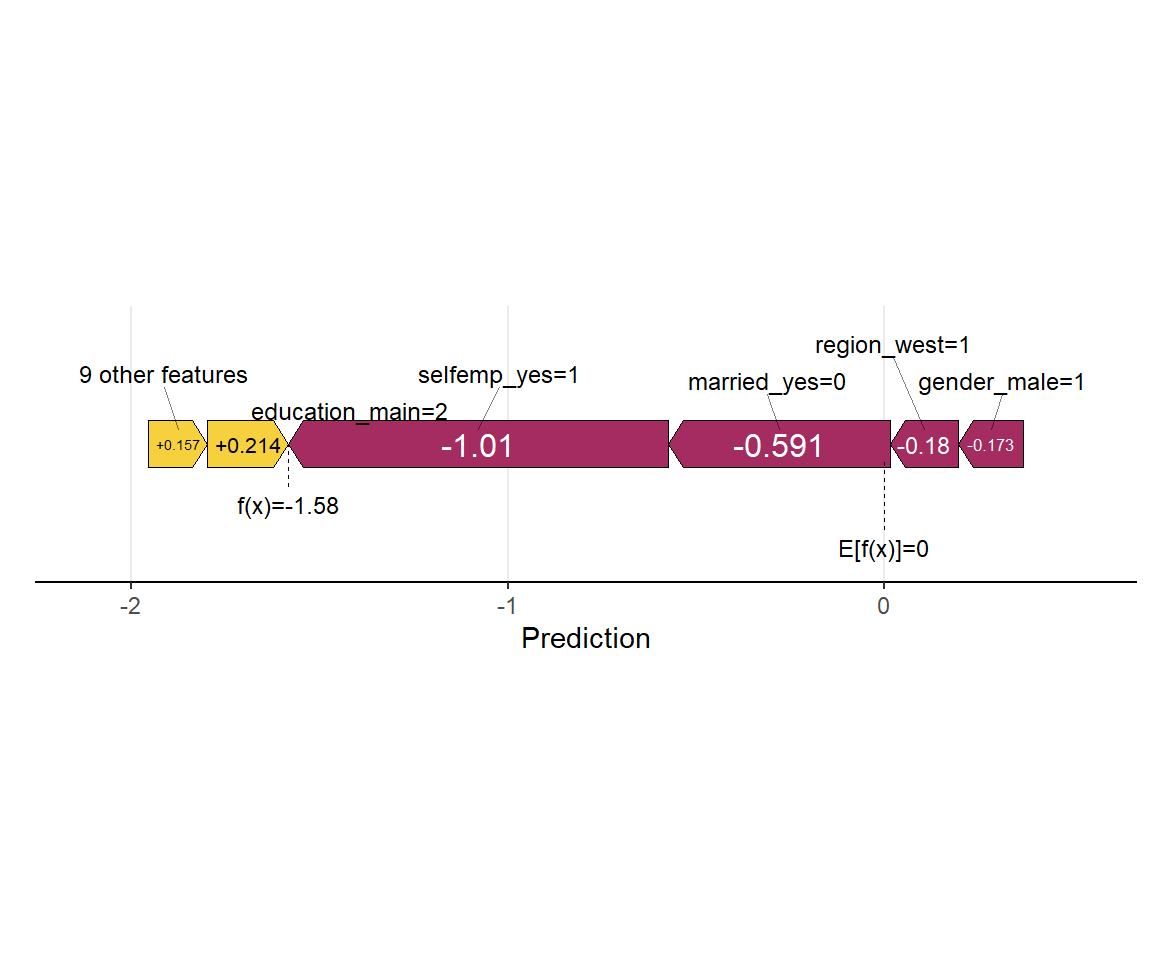

発展的な話題

対応パッケージ一覧

今回はtreeshapパッケージで計算したSHAPを使用しましたが、 shapvizパッケージが取り扱えるパッケージは他にもあります。

2024年8月時点で取り扱えるパッケージ・オブジェクトの一覧は次のとおり。

パッケージ名 クラス名
xgboost5 xgb.Booster
lightgbm lgb.Booster
h2o H2ORegressionModel
h2o H2OBinomialModel
h2o H2OModel
fastshap explain
treeshap treeshap
shapr explain
kernelshap kernelshap
kernelshap permshap
DALEX predict_parts

いずれもshapviz::shapviz関数で取り扱うことが出来ますが、引数には多少の差異があります。 詳細は Michael Mayer and Adrian Stando (2024c) を参照してください。

なお、Michael Mayer and Adrian Stando (2024c) にはSHAP値を格納した一般的なオブジェクトを shapvizパッケージに対応させる方法についても記載があります。

見た目の調節

shapvizパッケージの関数には見た目の調節を行うための引数がいくつか存在します。

また、内部的にggplot2パッケージが使用されていることから、 ggplot2の関数を用いた見た目の調節も可能です。

以下、例を示します6。

shapviz::sv_importance(sv, kind = "beeswarm",
                       max_display = 6, #6変数まで表示
                       show_numbers = TRUE, #SHAP Feature Importanceを印字
                       viridis_args = list(begin = 0.1, end = 0.9, option = "plasma")) + #色の設定
  ggplot2::theme_light()#ggplotのテーマの設定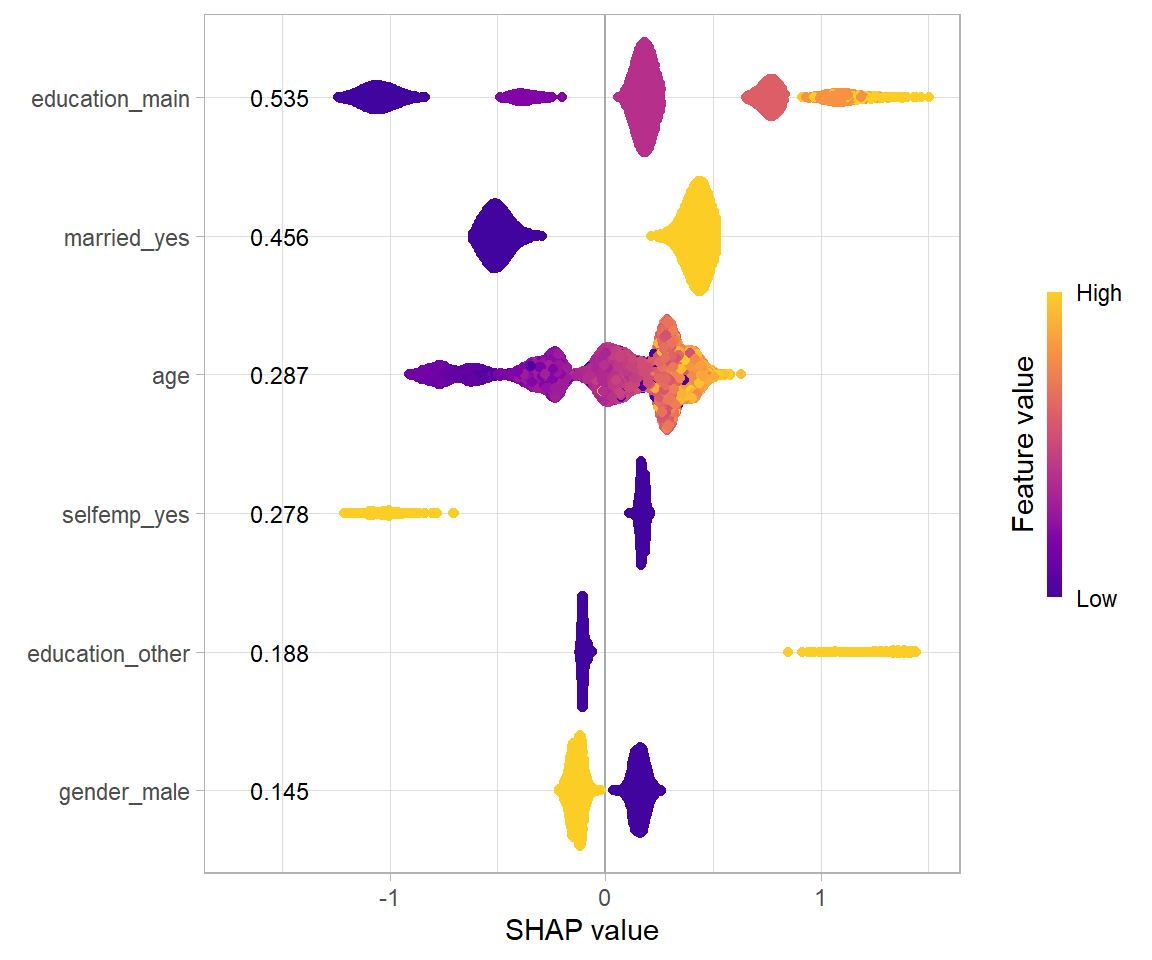

shapviz::sv_waterfall(sv, row_id = 1,
                      max_display = 14, #14変数まで表示
                      order_fun = function(s) 1:length(s), #並べ方を決める関数…ここでは元の並びを維持
                      fill_colors = c("black", "red"),#正側、負側の色指定
                      annotation_size = 5) + #下端のE[f(x)]と上端のf(x)の大きさ
  labs(title = "SHAP Waterfall Plot", subtitle = "row_id = 1") + #タイトル指定
  ggplot2::theme(plot.title = element_text(size=16)) #タイトルの大きさ指定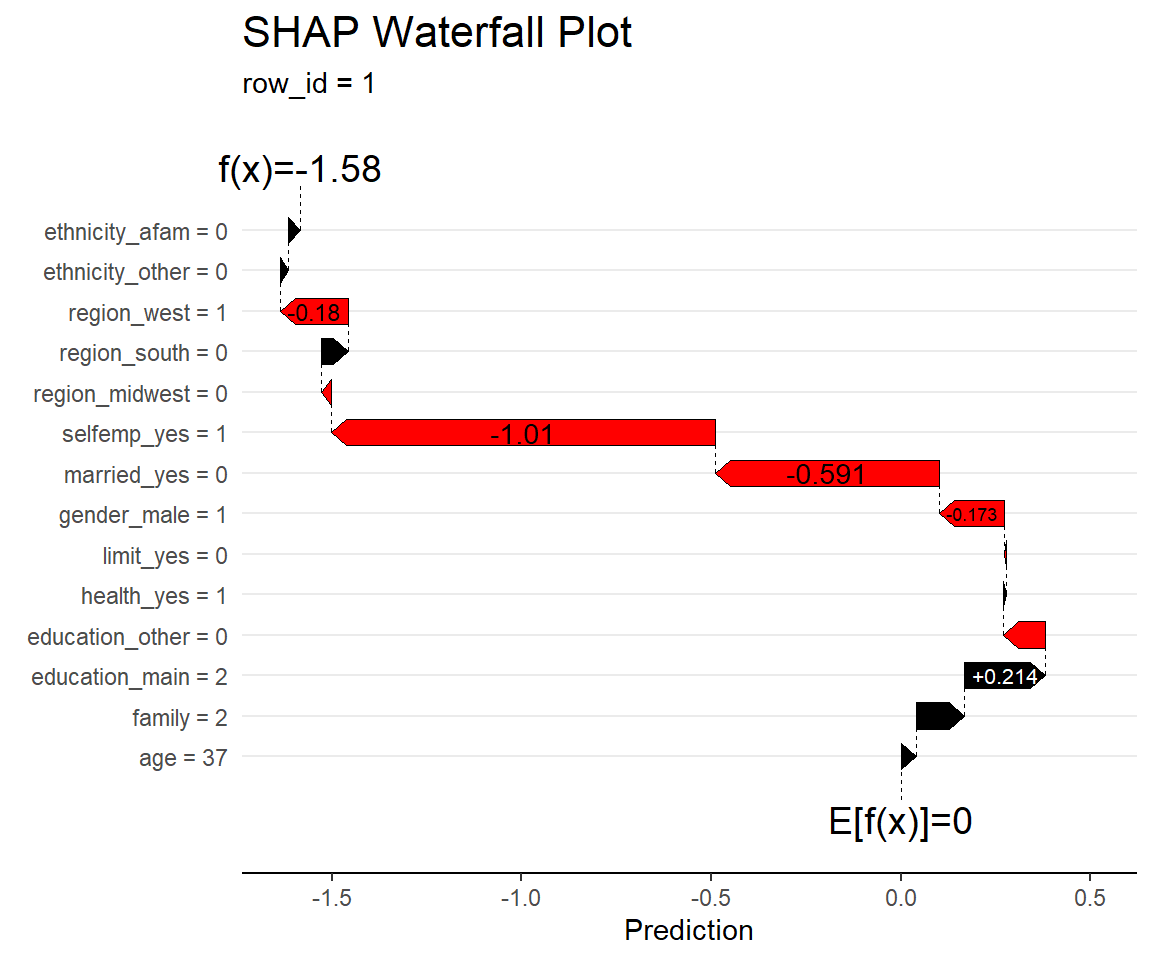

詳しくは各関数のドキュメンテーションを参照してください。

複数のSHAP値の取り扱い（mshapbizオブジェクト）

shapviz::shapviz関数で作られるオブジェクトはshapvizオブジェクトと呼ばれますが、 複数のshapvizオブジェクトを内包したmshapvizオブジェクトも存在し、 これもshapvizパッケージの関数でプロットすることが可能です。

mshapvizオブジェクトを得る方法はいくつかありますが、 たとえばsplit関数でshapvizオブジェクトを分割する方法があります。

svs <- split(sv, f = df_shap_x$education_main) #education_mainの値ごとに分割
shapviz::sv_dependence(svs, v = "age", color_var = NULL)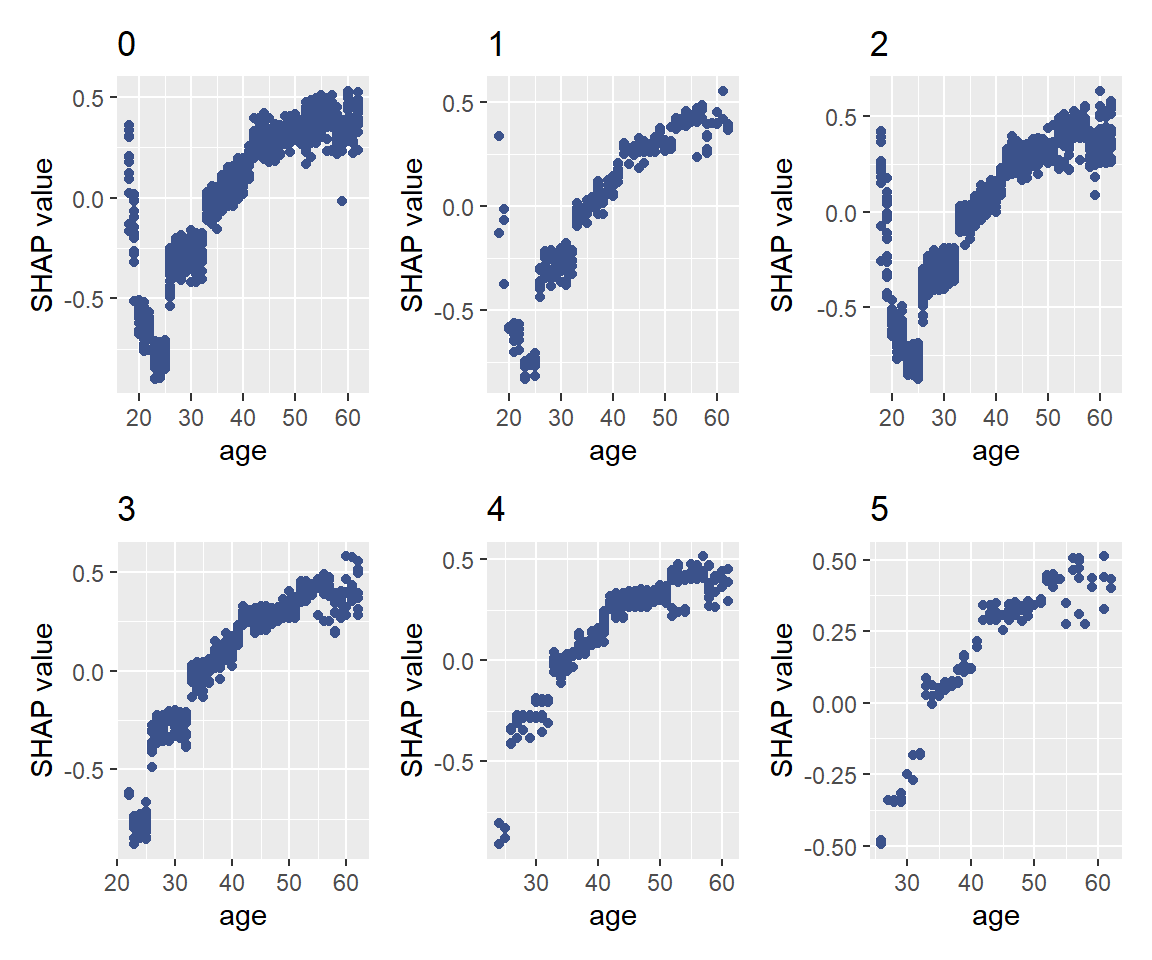

他には、shapvizオブジェクトをc関数で結合する方法もあります。

なお、shapvizオブジェクトの分割の際には、 データフレーム等と同じような変数[行, 列]記法を用いることが出来ます。

svs <- c(northeast = sv[df_shap_x$region_midwest+df_shap_x$region_south+df_shap_x$region_west==0, ],
         midwest = sv[df_shap_x$region_midwest==1, ],
         south = sv[df_shap_x$region_south==1, ],
         west = sv[df_shap_x$region_west==1, ])
shapviz::sv_dependence(svs, v = "age", color_var = NULL)

詳しくは Michael Mayer and Adrian Stando (2024b) を参照してください。

SHAP交互作用値（SHAP Interaction Plot）

ここまでに挙げたグラフは、すべて予測値の加法的な分解としてのSHAP値を様々な切り口でプロットしたものでした。

SHAP値は予測値への寄与を各説明変数に割り振ったものでしたが、 これとは別に、（2次の）交互作用への寄与を各2つの説明変数の組に割り振った、SHAP交互作用値(SHAP Interaction Values)というものもあります7。

SHAP交互作用値が計算できるパッケージは限られており、2024年8月時点ではtreeshapのみです。

t1 <- proc.time()
#interactionsをTRUEにしておく
shap_ts <- treeshap::treeshap(obj_uni, x = df_shap_x, interactions = TRUE)
t2 <- proc.time()
t0 <- (t2-t1)[3]
names(t0) <- NULL

cat("処理時間:", t0, "秒")
処理時間: 3.44 秒
sv_i <- shapviz::shapviz(shap_ts)

Summary Plotと同じように、説明変数の組ごとにSHAP交互作用値をプロットするには次のようにします。

#重要なものから3つを選び、3x3のプロットを作成
shapviz::sv_interaction(sv_i, max_display = 3, kind = "beeswarm")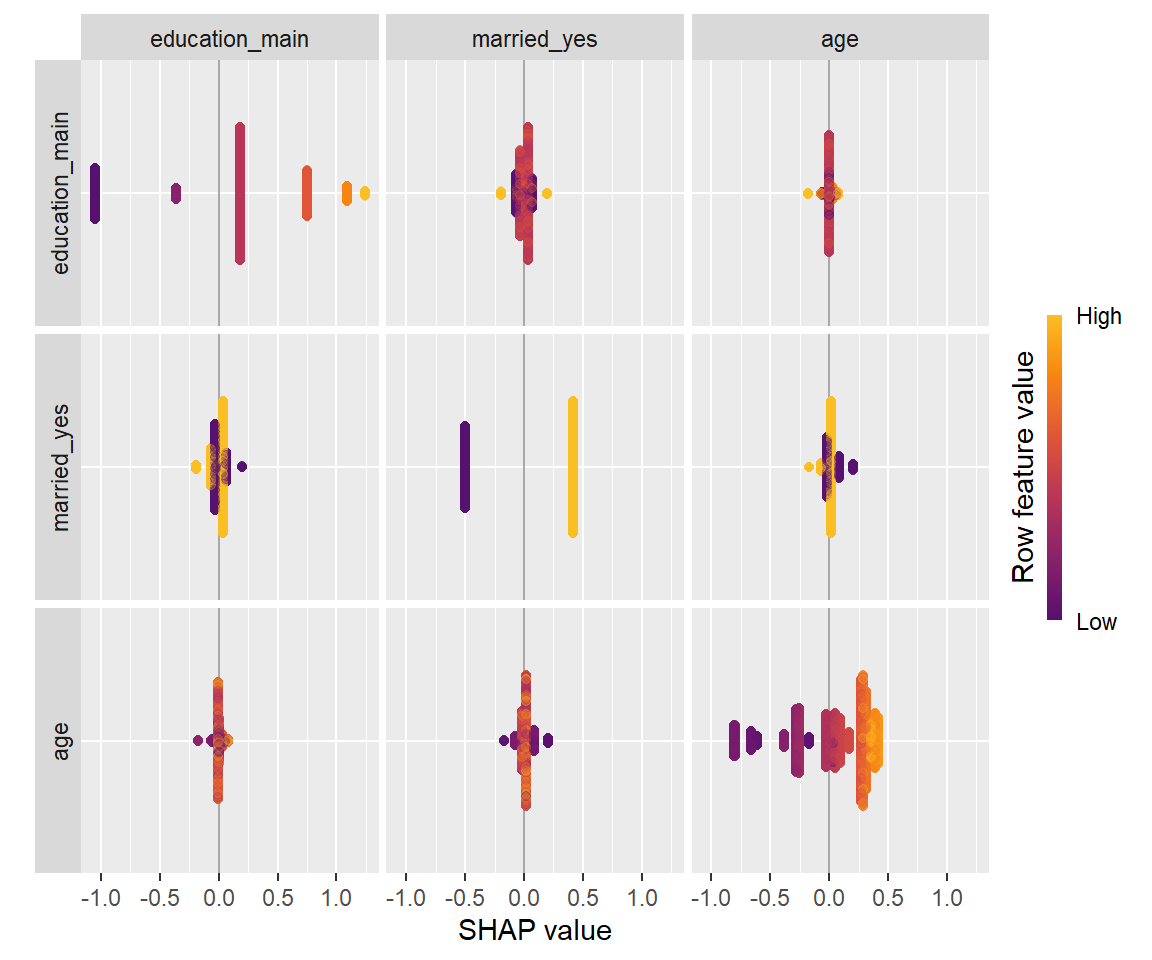

（左上から右下に至る）対角線のプロットはSummary Plotと同様に、予測値への寄与が大きさが横軸に示されています。 残るプロットが説明変数の組に対するSHAP交互作用値を横軸にプロットしたものです。

SHAP値のSummary Plotの場合は、交互作用が「SHAP値＝横軸方向のぶれ」となって表現されていたのに対し、 このプロットではSHAP交互作用値へ分解されているため、「ぶれ」が無くなっていることがわかります。 （たとえばeducation_mainのプロットでは、同じ学歴におけるSHAP値が同一となっている）

また、対角線を挟んで右上側にある3つと左下側にある3つについて、対称な位置にあるもの同士のグラフの形は同じですが、色分けが異なります。 例えば1行目・2列目のグラフ（education_main:married_yes）では学歴（education_main）で色分けされており、 最も低い層と高い層で交互作用が大きくなっていることが読み取れます。

なお、引数kindに"no"を与えた場合、Feature Importanceの類似物として、 SHAP交互作用値の絶対値の平均値を、行列の形で得ることが出来ます。 可視化には別の関数が必要です。ここではheatmap関数を用いてみます。

matrix_i <- shapviz::sv_interaction(sv_i, kind = "no")
matrix_i %>% heatmap(Rowv = NA, Colv = NA, revC = TRUE, symm = TRUE, margins = c(8,4))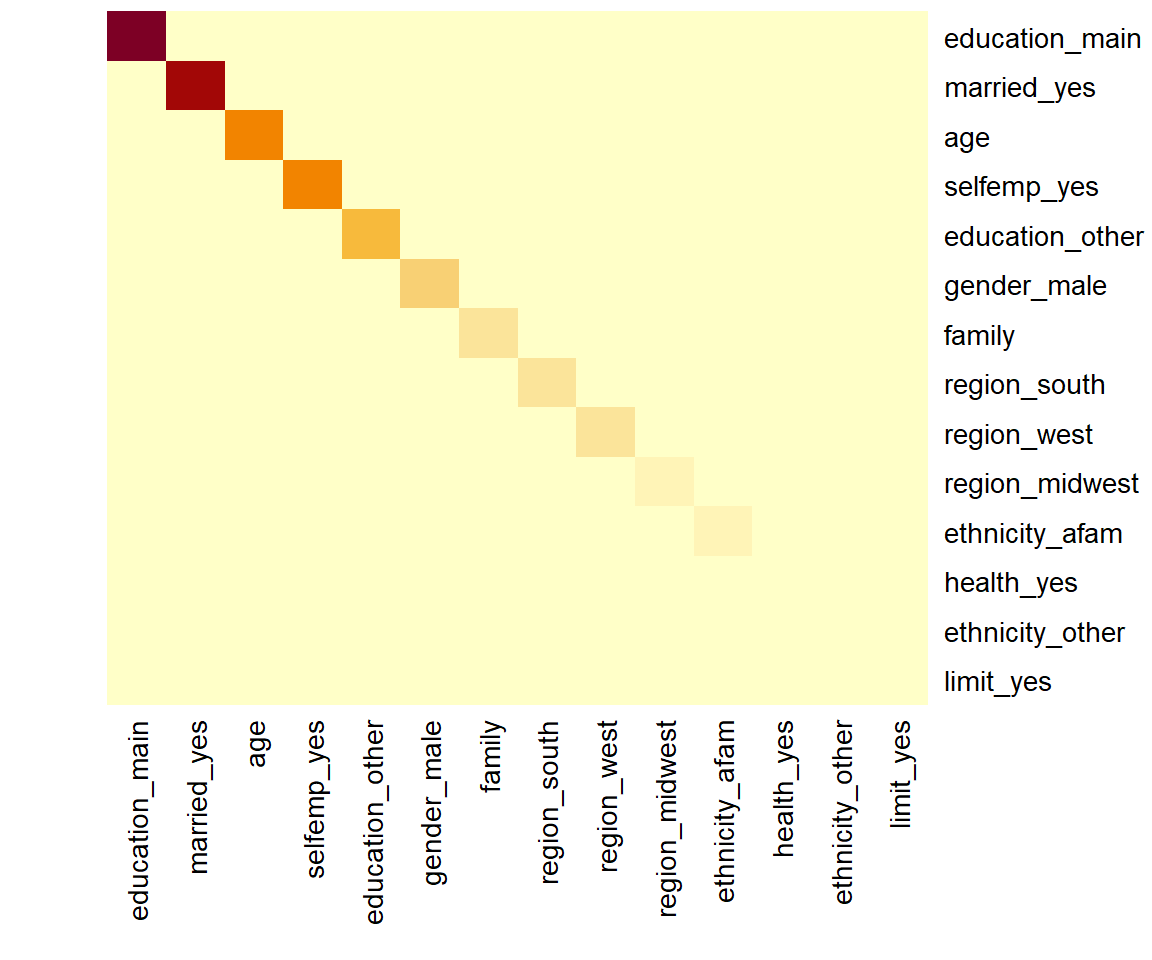

今回の例では交互作用があまり無い（XGBoostの予測値は、説明変数ごとに加法的に分解できるモデルとあまり変わらない）ということしか把握できませんでした。 敢えて対角線要素を除いてプロットするには次のようにします。

matrix_i2 <- matrix_i
diag(matrix_i2) <- 0
matrix_i2 %>% heatmap(Rowv = NA, Colv = NA, revC = TRUE, symm = TRUE, margins = c(8,4))

特定の説明変数の組に着目した分析を行う場合は、 前述のSHAP Dependence Plotで引数interactionsにTRUEを与えてSHAP交互作用値をプロットします。

shapviz::sv_dependence(sv_i, v = "age", color_var = "region_west", interactions = TRUE)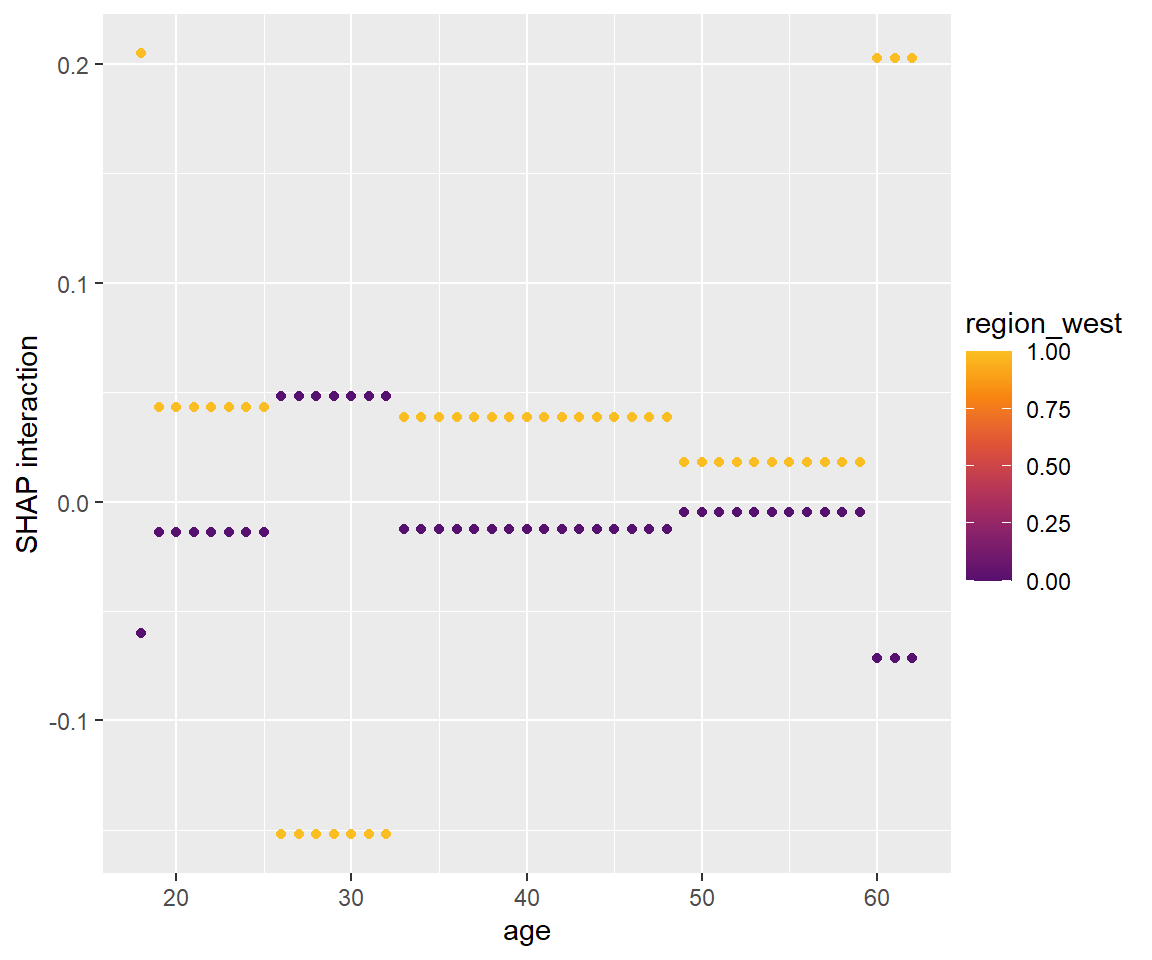

前述したような、居住地域が西側の場合、30歳前後での加入率が下がることが表現されています。 加えて、18歳や60歳以上では逆に加入率が上がるということをも可視化することができました。

なお、今回のモデルは木の構造が比較的単純なため、2次の交互作用ともなるとグラフもかなり単純なものになっています。

sv_dependence2D関数版もあります。 縦軸、横軸に説明変数をとり、SHAP交互作用値で色分けをするというもので、 先ほどのグラフから単に縦軸と色分けを逆転させただけです。

shapviz::sv_dependence2D(sv_i, x = "age", y = "region_west", interactions = TRUE)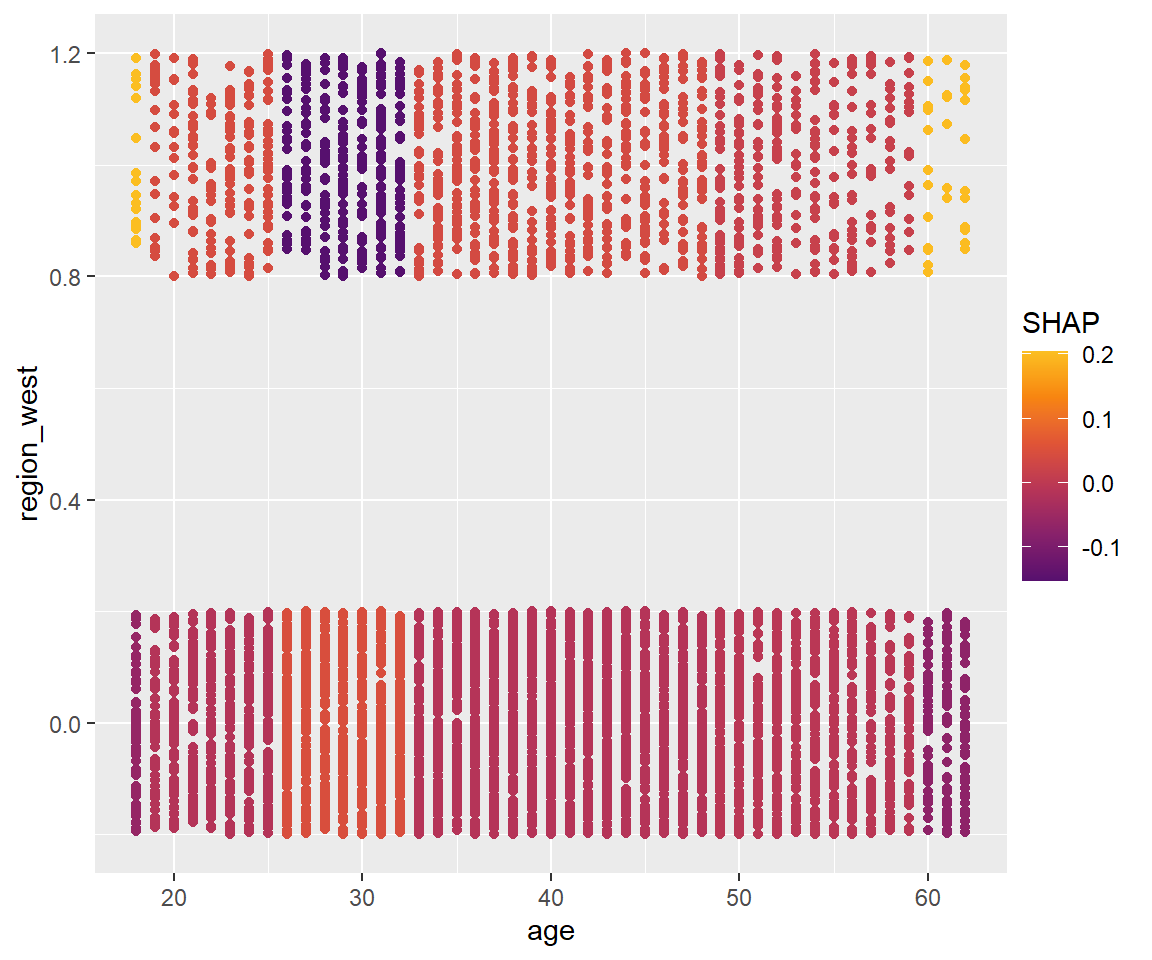

参考文献

  1. 元の研究は、自営業者の健康保険加入率の低さと健康状態の関係性を調べたものです。この研究で用いられた、1996年の米国医療費パネル調査(MEPS(Agency for Healthcare Research and Quality, n.d.))から抽出されたものがこのデータセットです。↩︎

  2. なお、ここではデータ前処理にrecipesパッケージを使用しています。 また、%>%はmagrittrパッケージによるパイプ演算子で、右辺の関数の第1引数に左辺を渡すという働きがあります。 たとえばa %>% f %>% g(b)という記述はg(f(a),b)と同等です。↩︎

  3. ハイパーパラメータは事前にチューニングしたものを入力しています。 チューニングの過程については本稿の主題を外れるので、割愛します。↩︎

  4. このプロットは下端に予測値の平均値がまず現れ、SHAP値（寄与）を順番に足していくと上端の予測値になるという構成になっています。 しかし、下端の予測値の平均値は、treeshapパッケージを用いる場合はデフォルトでは必ずゼロが表示される仕様です。 何かしらの数値を表示したい場合は、treeshap関数の引数baselineにその平均値を与える必要があります。 加えて、今回は2値分類モデルを構築した（学習時にobjective = "binary:logistic"と指定した）都合上、 SHAP値は確率予測値を分解したものではなく、確率予測値をロジット変換したものの分解になっています。 このため、上端に表示された予測値は確率予測値そのものにはなっていません。↩︎

  5. 実はXGBoostのモデルは、treeshapパッケージを明示的に用いずとも直接shapviz::shapviz関数を使用することが出来ます。 本稿では一般的な用法と同じ流れとなるよう、明示的にtreeshapパッケージを用いる形としました。↩︎

  6. 引数viridis_argsは、ggplot2::scale_colour_viridis_cに引き渡される引数をリストで指定するものです。 使用方法の詳細は H. Wickham (2024) や Bob Rudis, Noam Ross, and Simon Garnier (2024) を参照してください。↩︎

  7. SHAP値は「その説明変数が入力されていない場合とされた場合の予測値の差」の加重平均として計算します。これを、説明変数X, Yの組に対して「X,Y両方入力された場合 - Xが入力されてYが入力されない場合 - Yが入力されてXが入力されない場合 + X,Y両方入力されない場合」の加重平均と置き換えたものがSHAP交互作用値です。↩︎