yardstick

Author

データサイエンス関連基礎調査WG

Published

August 1, 2025

パッケージの概要

yardstickは機械学習や予測モデリングを行うためのパッケージ群tidymodelsに含まれており、構築したモデルの性能を評価するための指標(評価指標)を計算する機能を提供するパッケージです。様々な種類の評価指標に対応する関数が用意されていますので、構築したモデルやデータの性質、ビジネス上の目的を踏まえて、適切な指標を選択し使用していく必要があります。

基本的な使用方法

yardstickの基本的な使用方法を紹介します。テストデータとして、yardstickに含まれている二値分類用のテストデータtwo_class_exampleを使用します。 two_class_exampleは真のクラスtruthと予測クラスpredicted、及び両クラスに対するクラス確率の予測値からなるデータセットです。クラス確率の閾値が0.5に設定されており、クラス1のクラス確率を示すカラムClass1が0.5を超えているレコードに対しては予測クラスを示すpredictedカラムが”Class1”、Class2クラスが0.5を超えているレコードではpredictedが”Class2”となっています。

library(yardstick)
library(dplyr)  

data(two_class_example, package = "yardstick")
str(two_class_example)

'data.frame':   500 obs. of  4 variables:
 $ truth    : Factor w/ 2 levels "Class1","Class2": 2 1 2 1 2 1 1 1 2 2 ...
 $ Class1   : num  0.00359 0.67862 0.11089 0.73516 0.01624 ...
 $ Class2   : num  0.996 0.321 0.889 0.265 0.984 ...
 $ predicted: Factor w/ 2 levels "Class1","Class2": 2 1 2 1 2 1 1 1 2 2 ...

yardstickでは、評価指標ごとに対応する関数が用意されています。算出したい評価指標に対応する関数にデータセットを渡し、真値および予測値を示すカラムを指定するのが基本的な使用方法です。

ここでは例として、正しいクラスに分類できた件数の割合を表す指標Accuracyを計算します。評価指標Accuracyに対してはaccuracy関数が用意されており、次のとおり使用します。

two_class_example %>%
  accuracy(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.838

結果はtibble形式で、.metricは評価指標名、.estimatorは評価指標の計算方法、算出された評価指標の数値は.estimateというカラムで返されます。 Accuracyの値を見ると、two_class_exampleの予測クラスは約84%が真のクラスと一致していることがわかります。

なお各評価指標の計算関数は、上の例のように、計算したい予測値と真値をデータフレームで渡す関数のほかに、ベクトルでデータを渡すバージョンも用意されています。

accuracy_vec(truth = two_class_example$truth, estimate = two_class_example$predicted)

[1] 0.838

評価指標Accuracyの例を示しましたが、基本的な使用方法は他の評価指標の関数も同様です。以降では、回帰問題および分類問題にわけて、代表的な評価指標と対応するyardstickの関数の使用例を紹介していきます。

回帰問題の評価指標

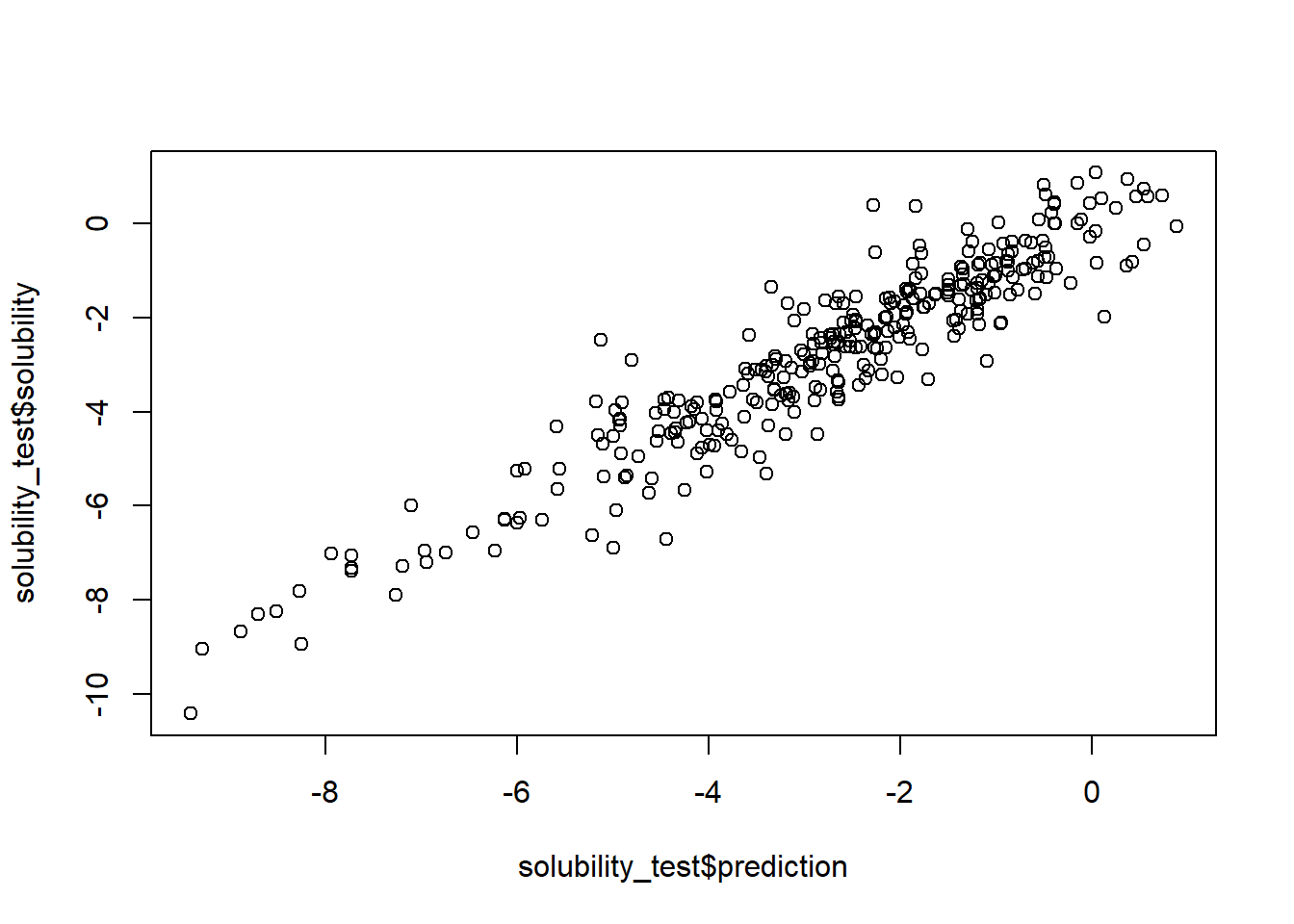
数値データを予測する回帰問題における、代表的な評価指標とyardstickによる使用例を紹介します。サンプルデータとして、yardstickで用意されているsolubility_testデータを用います。 solubility_testデータは、数値型の真値solubilityと予測値predictionの二つのカラムを持つデータセットです。

data("solubility_test", package = "yardstick")
str(solubility_test)

'data.frame':   316 obs. of  2 variables:
 $ solubility: num  0.93 0.85 0.81 0.74 0.61 0.58 0.57 0.56 0.52 0.45 ...
 $ prediction: num  0.368 -0.15 -0.505 0.54 -0.479 ...

plot(x=solubility_test$prediction, y=solubility_test$solubility)

MAE
MAE(Mean Absolute Error)は次式のとおり、真の値と予測値との差の絶対値について平均を取った指標です。すなわち、真の値に対して予測値が平均的にどの程度ずれているのかを評価する指標となっています。ここで、Nはデータの件数、y_iと\hat{y_i}はそれぞれデータiに対する真の値および予測値を表します。

\frac{1}{N}\sum_{i=1}^{N}|y_i-\hat{y_i}|

solubility_test %>%
  mae(truth = solubility, estimate = prediction)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard       0.545

RMSE
RMSE(Root Mean Squared Error)は真値と予測値との差の二乗の平均を取った指標(MSE)の平方根です。誤差の二乗をもとに計算した指標なので、予測値のずれが大きなデータに対してはMAEよりも大きな値が加算されることになります。したがって、外れ値や誤差が大きくなることに対して、より大きなペナルティを課したい場合に適切な指標指標と考えられます。

\sqrt{\frac{1}{N}\sum_{i=1}^{N}(y_i-\hat{y_i})^2}

solubility_test %>%
  rmse(truth = solubility, estimate = prediction)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       0.722

決定係数
決定係数は、目的変数のばらつき(総変動)のうち説明変数により説明される割合で、モデルの当てはまりの良さを示す指標として使用されます。

solubility_test %>%
  rsq(truth = solubility, estimate = prediction)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rsq     standard       0.879

yardstickのrsq関数は相関係数の二乗として実装されており、(0, 1)の範囲を取ります。一方、rsq_tradは1-残差変動/総変動として計算されているバージョンです。両者は線形回帰モデルでない場合一致せず、また線形回帰モデル以外にrsq_tradを適用すると値が負になる可能性もある等、特に線形モデル以外への決定係数の適用とその解釈には注意が必要です。

solubility_test %>%
  rsq_trad(truth = solubility, estimate = prediction)

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 rsq_trad standard       0.879

分類問題の評価指標

続いて、分類問題に関する評価指標とyardstickによる使用例を紹介します。ここでもサンプルデータとして、冒頭で紹介したtwo_class_exampleを使用します。なおtwo_class_exampleデータがそうなっているように、分類問題の評価指標の関数に渡す真値および予測値はfactor型でなければなりません。

混同行列
最初に、分類問題における代表的な評価指標の計算に使用される、混同行列(Confusion Matrix)を紹介します。混同行列は、真のクラスと予測クラスの組み合わせでデータ件数を分割表にまとめたもので、yardstickではconf_mat関数で出力することができます。

two_class_example %>%
  conf_mat(truth = truth, estimate = predicted)

          Truth
Prediction Class1 Class2
    Class1    227     50
    Class2     31    192

陽性(positive)と陰性(negative)とで判別する二値分類の混同行列は２×２の分割表となりますが、一般的に以下の名称でまとめられます。

2 \times 2 confusion matrix.
		Truth
		Positive	Negative
Prediction	Positive	TP(true positive)	FP(false positive)
Prediction	Negative	FN(false negative)	TN(true negative)

以降では、2×2の混同行列を前提として、上表の表記で評価指標を紹介していきます。

Accuracy(正解率)
冒頭でも紹介した評価指標Accuracyは、真のクラスがpositiveのデータを正しくpositiveと予測できた、または真のクラスがnegativeのデータを正しくnegativeと予測できた件数の割合ですので、混同行列からは以下の通り計算されます。

\frac{TP+TN}{TP+TN+FN+FP} yardstickでの実行例は次のとおりです。(冒頭で紹介したものと同じです。)

two_class_example %>%
  accuracy(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy binary         0.838

Accuracyはわかりやすい指標ですが、クラスごとの件数に偏りがある不均衡データの場合には注意が必要です。例えば、Class1が全体の95%を占めるようなデータの場合、「全てのデータを一律Class1と予測する」モデルのAccuracyは95%という一見高い数値となります。これがもし、少数のクラス(Class2)が重要であり、Class2を正しく識別したいような問題の場合、Accuracyは適切な評価指標とは言えないでしょう。

Precision(適合率)
Precisionは、positiveと予測したデータのうち真のクラスがpositiveであった割合を示す指標で、具体的には以下の通りです。

\frac{TP}{TP+FP} yardstickではprecision関数で計算します。真値及び予測値のfactor型変数において、2クラスのうちどちらをpositiveとして計算するかは、event引数に”first”または”second”を渡して指定することができ、省略した場合のデフォルトは”first”です。このevent引数によるpositiveクラスの設定方法に関しては、以降で紹介する分類用の評価指標関数において同様です。

two_class_example %>%
  precision(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision binary         0.819

Precisionは予測値がpositiveであるデータに着目した評価指標なので、偽陽性(FP)を減らしたい場合に有効です。スパムメールの分類においてスパムをpositiveとして判別したい場合や、あるサービスについて解約が見込まれる顧客をpositiveと予測し何らかのコストのかかる施策を打って対応する場合等、positiveと予測するからには高い的中率でありたい状況での適用が考えられます。

Recall(再現率)
Recallは真の値がpositiveのデータのうち、正しくpositiveと予測したデータの割合です。算式とyardstickによる実行例は以下の通りです。

\frac{TP}{TP+FN}

two_class_example %>%
  recall(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 recall  binary         0.880

Recallは真の値がpositiveのデータに着目した評価指標なので、例えばpositiveデータの割合が小さい不均衡データにおいて、真の値がpositiveであるデータを見逃さないようにしたい、といった状況で有効です。

F-β score
PrecisionとRecallは着目する観点が異なっていましたが、どちらも考慮した評価指標としてF-β scoreがあります。算式は次の通りで、\betaはRecallとPrecisionのどちらを重視するかを調整するパラメータです。両者に差をつけない\beta=1のとき、F-1 score呼ばれます。

\frac{(1+\beta^2)\times Recall \times Precision}{\beta^2 \times Precision + Recall} yardstickではf_meas関数で算出しますが、パラメータbetaを引数として渡すことができます。以下はF-1 scoreの算出例です。(betaのデフォルトは1なので、以下の場合省略も可能です。)

two_class_example %>%
  f_meas(truth = truth, estimate = predicted, beta = 1)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 f_meas  binary         0.849

Specificity
Recallは真値がpositiveのデータに着目して、正しくpositiveと予測できた割合を示す指標でしたが、同様の考え方で真値がnegativeのデータに着目した指標がSpecificityです。

\frac{TN}{TN+FP}

two_class_example %>%
  spec(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 spec    binary         0.793

ROC AUC
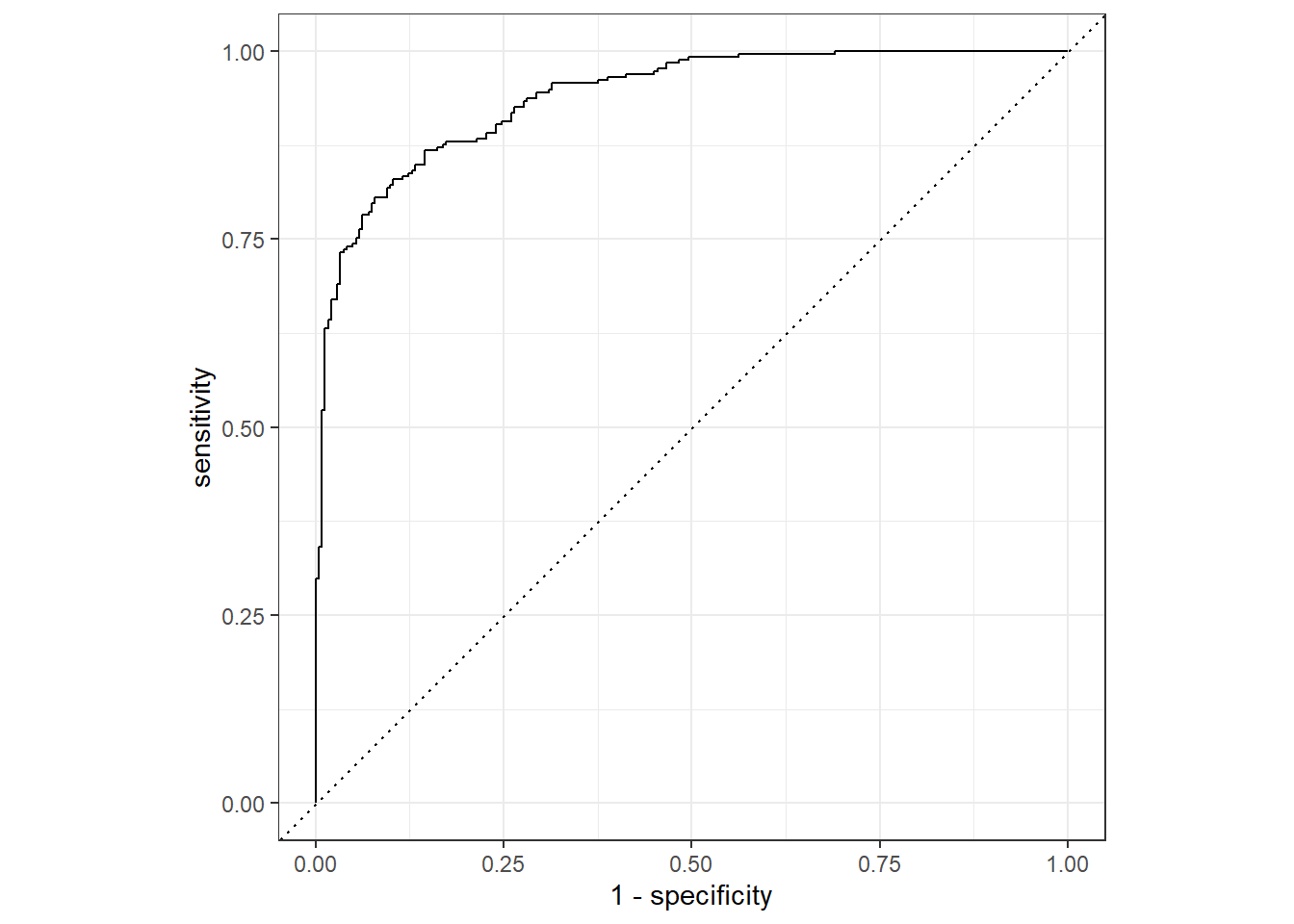
ここまでの指標は、予測クラスをpositiveクラスとnegativeクラスのどちらかに分けた状態を前提としていました。実際には、多くのモデルは両クラスに属する確率(クラス確率)を算出し、例えばpositiveクラスのクラス確率が一定の閾値を上回ったデータについてpositiveと判定する、といった処理が行われることも多いでしょう。クラス確率に対する閾値を変えると、予測クラスが変わり混同行列も変化しますので、モデルの全体としての適切性にも影響を与えることになるでしょう。

このような、閾値の変化に対するモデルの予測結果の変化を可視化する方法として、ROC曲線(Receiver Operatorating Characteristic curve)という方法があります。 ROC曲線は、positiveクラスのクラス確率に対する閾値を1(全てのデータをnegativeと予測)から0(全てのデータをpositiveと予測)へと徐々に変化させたときの、各閾値における真陽性率(=Recall=Sensitivity)を縦軸、偽陽性率(=1-Specificity)を横軸としてプロットしたものです。 yardstickでは、ggplot2パッケージのautoplot関数を利用してROC曲線を描画するための、roc_curve関数が用意されています。

library(ggplot2)

two_class_example %>%
  roc_curve(truth, Class1) %>%
  autoplot()

分類の精度が良いモデルでは、多くの閾値において真陽性率(真のクラスがpositiveのときに正しくpositiveと分類できる割合)が高く、偽陽性率(真のクラスがnegativeのときに誤ってpositiveと分類する割合)が低いこと、すなわちROC曲線が左上に広がっている状態が期待されるでしょう。逆に完全にランダムな分類器では、真のクラスがpositiveであろうとnegativeであろうと、等確率でpositiveに分類することになりますので、ROC曲線は傾き1の直線(上図の点線)となります。

ROC曲線の下部の面積(AUC; Area Under Curve)を測ることで、上の議論を定量的に評価することができます。 AUC=0.5はランダムな分類器に対応し、AUCが1に近づくほど、多くの閾値でよい分類性能を示していることになります。

two_class_example %>%
    roc_auc(truth, Class1)

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 roc_auc binary         0.939

Log loss
クラス確率を使用して評価する他の指標として、Log lossを紹介します。 Log lossは以下の式で計算され、各データにおいて正解クラスに対して高いクラス確率を予測できていると小さい値が、誤ったクラスに対して高いクラス確率を予測していると大きな値が加算されます。そのため、数値が小さいほど精度の高いモデルということになります。

-\frac{1}{N}\sum^{N}_{i=1}[y_i\log(p_i)+(1-y_i)\log(1-p_i)] ここでNはデータ数、y_iはデータiに対する正解ラベル(1 or 0)、p_iはクラスy=1に対するクラス確率です。
yardstickでは以下のとおり計算できます。

two_class_example %>%
  mn_log_loss(truth = truth, Class1)

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 mn_log_loss binary         0.328

Log lossは予測したクラス確率を直接評価する指標なので、モデルで予測した確率を用いて期待値を計算するような場合等で有効な指標と考えられます。ただし、確率に着目しているが故に、閾値を設けて分類まで行うような問題では、以下のようなケースが発生し得ることに注意が必要です。

# 2データの2クラス分類問題
y <- factor(c(1, 1), levels = c(1, 2)) # 正解クラスは両データとも1
p1 <- c(0.99, 0.49)  # モデル1のクラス1確率の予測値
p2 <- c(0.51, 0.51)  # モデル2のクラス1確率の予測値

logloss_1 <- mn_log_loss_vec(y, p1)
logloss_2 <- mn_log_loss_vec(y, p2)
cat("model 1: ", logloss_1, "\nmodel 2: ", logloss_2)

model 1:  0.3617001 
model 2:  0.6733446

この例では、高い確信度をもって1データ目をクラス1と予測している、モデル1のLog lossの数値が小さくなっています。一方で、仮に閾値を0.5として分類まで行うような場合では、モデル2は両データとも正解ですが、モデル1ではデータ2は不正解となり、Log lossによる判断とは逆の結果となります。このように、閾値を設けて分類まで行うような状況では、クラス確率の予測値そのものに着目するLog lossよりも、クラス確率の順序関係を重視しているROC AUCを使用することが考えられます。

多クラス分類
ここまでは二値分類を前提として評価指標を紹介してきましたが、多クラス分類についても簡単に紹介します。次の例ではyardstickの多クラス分類用のテストデータhpc_cvを用います。このデータセットは4クラスの分類を行うためのもので、真のクラスであるobs、予測クラスpred、各クラスのクラス確率の予測値のカラムを持ちます。更に、データを分割しての検証(クロスバリデーション)を意図した、グループを示すカラムResampleが用意されています。

data(hpc_cv, package = "yardstick")
str(hpc_cv)

'data.frame':   3467 obs. of  7 variables:
 $ obs     : Factor w/ 4 levels "VF","F","M","L": 1 1 1 1 1 1 1 1 1 1 ...
 $ pred    : Factor w/ 4 levels "VF","F","M","L": 1 1 1 1 1 1 1 1 1 1 ...
 $ VF      : num  0.914 0.938 0.947 0.929 0.942 ...
 $ F       : num  0.0779 0.0571 0.0495 0.0653 0.0543 ...
 $ M       : num  0.00848 0.00482 0.00316 0.00579 0.00381 ...
 $ L       : num  1.99e-05 1.01e-05 5.00e-06 1.56e-05 7.29e-06 ...
 $ Resample: chr  "Fold01" "Fold01" "Fold01" "Fold01" ...

多クラス分類のデータに対しても、一部の関数は二値分類と同じように適用することができます。以下では、hpc_cvデータのFold01に対して、正しく真のクラスを予測できている割合Accuracyを計算しています。

hpc_cv %>%
  filter(Resample == "Fold01") %>%
  accuracy(obs, pred)

# A tibble: 1 × 3
  .metric  .estimator .estimate
  <chr>    <chr>          <dbl>
1 accuracy multiclass     0.726

PrecisionやRecall等の多クラス分類への拡張方法はいくつかありますが、ここでは、これら関数のデフォルトに設定されているMacro averagingをいう方法を紹介します。 Macro averagingでは、複数あるクラスごとに「当該クラス」対「それ以外のクラス」の二値分類として評価指標を計算し、計算した指標について全クラスの平均を取る方法です。すなわち、kクラスの分類では、Pr_{1}を「クラス1」と「それ以外のクラス」の二値分類に関して計算したPrecision、Pr_{2}を「クラス2」と「それ以外のクラス」に対するPrecision、というようにkクラスの計算を行った上で以下のとおり平均を取った指標です。 \frac{Pr_1+Pr_2+\dots+Pr_k}{k} yardstickのprecision関数は、多クラス分類用のデータを渡すと自動的に多クラス分類用の計算を行ってくれます。引数estimatorに”macro”を設定することでMacro averagingを明示的に指定することができますが、多クラス分類用のデータを与えるとデフォルトでMacro averagingが計算されるため省略可能です。

hpc_cv %>%
  filter(Resample == "Fold01") %>%
  precision(obs, pred)

# A tibble: 1 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 precision macro          0.637

ここまでいくつかの評価指標を紹介してきましたが、yardstickには他にも様々な評価指標が用意されていますので、必要に応じてyardstickの公式サイトをご参照ください。

その他便利な機能

グループ別の評価指標の計算

hpc_cvデータはクロスバリデーション用のグループを示すResampleカラムが用意されていました。 yardstickの各評価指標の関数は、dplyerパッケージのgroup_by関数によりグループ化することで、グループごとの評価指標を計算することができます。以下ではResampleカラムでグループ化し、グループごとのAccuracyを計算しています。

hpc_cv %>%
  group_by(Resample) %>%
  accuracy(obs, pred)

# A tibble: 10 × 4
   Resample .metric  .estimator .estimate
   <chr>    <chr>    <chr>          <dbl>
 1 Fold01   accuracy multiclass     0.726
 2 Fold02   accuracy multiclass     0.712
 3 Fold03   accuracy multiclass     0.758
 4 Fold04   accuracy multiclass     0.712
 5 Fold05   accuracy multiclass     0.712
 6 Fold06   accuracy multiclass     0.697
 7 Fold07   accuracy multiclass     0.675
 8 Fold08   accuracy multiclass     0.721
 9 Fold09   accuracy multiclass     0.673
10 Fold10   accuracy multiclass     0.699

複数評価指標のセット化

yardstickのmetric_set関数を使用すると、複数の評価指標をまとめて1セットとした評価指標の関数を作成することができます。以下では、二値分類問題に対する三つの評価指標をまとめた新たな評価指標関数を作成し、two_class_exampleデータに適用しています。

class_metrics <- metric_set(accuracy, precision, recall)
two_class_example %>%
  class_metrics(truth = truth, estimate = predicted)

# A tibble: 3 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 accuracy  binary         0.838
2 precision binary         0.819
3 recall    binary         0.880

metric_setは、データに対して複数の評価指標を一度に適用したいときに便利ですが、セットとしてまとめる評価指標は同じ問題に適用できるものでなければなりません。例えば回帰問題用のデータに使用するMAEの関数と、分類問題用のデータに使用するLog lossの関数とをmetric_setでまとめようとすると、エラーになるためご注意ください。

# 以下は実行時エラー
# error_metric_set <- metric_set(mn_log_loss, mae)

なお、yardstickには基本的な評価指標をいくつかまとめたセットがmetrics関数として既に用意されています。 metrics関数は、データの種類ごとにあらかじめ設定されている指標を計算して返してくれます。例えば、二値分類と回帰については、それぞれ以下に示す指標が返されます。

# 二値分類
two_class_example %>%
  metrics(truth = truth, estimate = predicted, Class1)

# A tibble: 4 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 accuracy    binary         0.838
2 kap         binary         0.675
3 mn_log_loss binary         0.328
4 roc_auc     binary         0.939

# 回帰
solubility_test %>%
  metrics(truth = solubility, estimate = prediction)

# A tibble: 3 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       0.722
2 rsq     standard       0.879
3 mae     standard       0.545

パラメータ調整済の評価指標関数の作成

先に紹介したように、F-β scoreはパラメータ\betaを調整することでRecallとPrecisionのどちらを重視するかをコントロールできる指標で、対応するf_meas関数には引数betaとして指定できるものでした。 f_measのように、実行時にパラメータを渡す評価指標は、metric_tweak関数を使用することで、あらかじめ所定のパラメータをセットした状態の関数を作ることができます。

# beta = 0.5の関数F-β関数を作成
f_05_score <- metric_tweak("F-0.5 score", f_meas, beta=0.5)
two_class_example %>%
  f_05_score(truth = truth, estimate = predicted)

# A tibble: 1 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 F-0.5 score binary         0.831

これは複数のパラメータの組み合わせでmetric_setを作成したい場合等に便利です。

# betaの値ごとのF-β scoreを計算
f_1_score <- metric_tweak("F-1 score", f_meas, beta=1)
f_2_score <- metric_tweak("F-2 score", f_meas, beta=2)
f_beta_metric <- metric_set(f_05_score, f_1_score, f_2_score)
two_class_example %>%
  f_beta_metric(truth = truth, estimate = predicted)

# A tibble: 3 × 3
  .metric     .estimator .estimate
  <chr>       <chr>          <dbl>
1 F-0.5 score binary         0.831
2 F-1 score   binary         0.849
3 F-2 score   binary         0.867

参考資料

[1] Kuhn et al., (2020). Tidymodels: a collection of packages for modeling and machine learning using tidyverse principles. https://www.tidymodels.org.
[2] Kuhn M, Vaughan D, Hvitfeldt E (2025). yardstick: Tidy Characterizations of Model Performance. R package version 1.3.2, https://yardstick.tidymodels.org, https://github.com/tidymodels/yardstick.